交流_補足

誘導起電力の計算の補足

微積を使わない

本編の式　V = - Φ₀\(\large{\frac{Δ\cosωt}{Δt}}\)　を微積を使わずに計算する方法を説明します。

なぜ単純に約分してはいけないか

似た計算は『磁場を横切る導線』項でもやっていて、そのときは、

　　V = \(\large{\frac{ΔΦ}{Δt}}\)　の分子に

　　ΔΦ = BΔS = BlvΔt = vBlΔt　を代入して

　　V = \(\large{\frac{ΔΦ}{Δt}}\) = \(\large{\frac{vBlΔt}{Δt}}\) = vBl

と計算しました。しかし今回はそうはいきません。\(\large{\frac{Δ\cosωt}{Δt}}\) = \(\large{\frac{\cosωΔt}{Δt}}\) = cosω とは計算できないからです。

たとえば角度が 30° から2倍の 60° になったときに、cos は \(\large{\frac{\cos60°}{\cos30°}}\) ≒ ≒ 0.57 倍です。2倍にはなりません。cos の中身と外身は変化の仕方が違います。

ですから　Δcosωt　はちゃんと　cosω(t + Δt) - cosωt　と変形しなければなりません。これならば　cosωt　の微小変化量といえます。

前提となる知識

計算を進める上で次のような三角関数の知識が必要となります。数学の教科書に載ってます。

三角関数の加法定理　（４つの式のうち３番目の式を使います。）

　　　　sin(α + β) = sinαcosβ + cosαsinβ

　　　　sin(α - β) = sinαcosβ - cosαsinβ

　　　　cos(α + β) = cosαcosβ - sinαsinβ

　　　　cos(α - β) = cosαcosβ + sinαsinβ

ωΔt が極めて小さいとき、

　　　　cosωΔt ≒ 1

　　　　sinωΔt ≒ ωΔt

（たとえば　cos0.01 ≒ 1　であり、sin0.01 ≒ 0.01　です。）

それでは計算してみます

　　　　Δcosωt = cosω(t + Δt) - cosωt

　　　　　　 　 = cos(ωt + ωΔt) - cosωt

　　　　　　 　 = cosωt⋅cosωΔt - sinωt⋅sinωΔt - cosωt

　　　　　　 　 = cosωt⋅1 - sinωt⋅ωΔt - cosωt

　　　　　　 　 = - sinωt⋅ωΔt

　　　　　　 　 = - ωΔt sinωt

　∴　　V = - Φ₀\(\large{\frac{Δ\cosωt}{Δt}}\) = - Φ₀\(\large{\frac{-ωΔt\sinωt}{Δt}}\) = - Φ₀ (- ωsinωt) = Φ₀ωsinωt

となり、本編の計算結果と一致します。

（実はここまでの計算自体が cos x の微分を求める計算そのものであったりします。(cos x)' = - sin x であり、(cos2x)' = - 2sin2x です。）

V = vBl を使って誘導起電力の大きさを求める

本編では電磁誘導の法則

　　　　V = - \(\large{\frac{ΔΦ}{Δt}}\)

を使って回転するコイルの誘導起電力を求めましたが、もう一つ、『磁場を横切る導線』項、『電磁誘導とローレンツ力』項で紹介した磁場を横切る導線に生じる誘導起電力が「 V = vBl 」であることを使って求める方法があります。

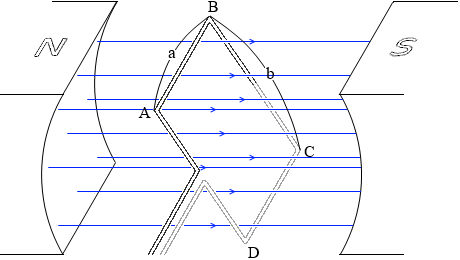コイルが長方形であるとし、角を順番にABCDとし、AB = a [m] 、BC = b [m] とし、磁束密度を B [Wb/m²] 、コイルの回転の角速度を ω [rad/s] 、コイル面の法線と磁場の向きとのなす角を θ [rad]（=ωt）とします。

このとき、誘導起電力が生じるのはABとCDだけです。BCとDAには誘導起電力は生じません。磁場を横切ってないからです。磁束を刈り取ってないからです。『斜めに横切る場合』の cosθ が cos90° になっていることになります。電磁誘導のおおもとはローレンツ力であり、磁場を横切らないとローレンツ力は発生しません。＊厳密な話をすると、導線BC、導線DA内に存在する電荷にまったくローレンツ力がはたらかないわけではありません。ローレンツ力の方向が導線に垂直な方向であり、『電磁誘導とローレンツ力』項のような電荷分布の偏りが起こらず、BC間、DA間に電位差が生じないのです。
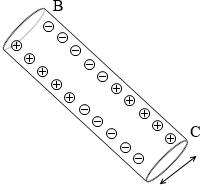この方向に電位差が生じても意味が無い。

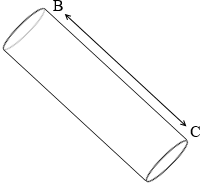こちら方向に電位差が生じていれば、コイルの起電力として寄与していた。
　閉じる

ABに生じる誘導起電力を「 V = vBl 」を使って求めてみます。まず v を求めます。

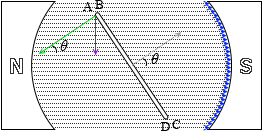導線ABが周回する速さは（半径）×（角速度）だから \(\large{\frac{b}{2}}\) × ω で、このうち磁場に垂直な成分は sinθ を掛けて \(\large{\frac{b}{2}}\)ωsinθ であり、θ = ωt を代入すると \(\large{\frac{b}{2}}\)ωsinωt となり、これが求める v です。

「 V = vBl 」の l はここでは a のことだから、求める誘導起電力 V_AB は、

　　　　V_AB = \(\large{\frac{b}{2}}\)ωsinωt⋅B⋅a

同様に V_CD も、

　　　　V_CD = \(\large{\frac{b}{2}}\)ωsinωt⋅B⋅a

コイル全体の誘導起電力 V は、

　　　　V = V_AB + V_CD

　　　　　= bωsinωt⋅B⋅a

　　　　　= B⋅ab⋅ωsinωt

コイルの面積を S [m²] とし、θ (=ωt) = 0 すなわちコイル面と磁場が垂直のときのコイルを貫く磁束を Φ₀ [Wb]（=BS）とすると、

　　　　V = B⋅ab⋅ωsinωt

　　　　　= B⋅S⋅ωsinωt

　　　　　= Φ₀ωsinωt

となり、本編と同じ結果が得られます。