電流がつくる磁場_補足

各磁場の式の導出

本編で示した、直線電流がつくる磁場の式、円形電流がつくる磁場の式、ソレノイドがつくる磁場の式は、アンペールの法則やビオ・サバールの法則というものによって導かれます。導出方法については高校生は覚えなくていいのですが、一応ここで説明しておきます。

アンペールの法則

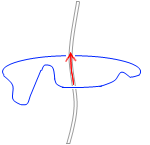電流の大きさは、それを取り囲むループに沿った各点の磁場を足し合わせた総和に比例する、という法則があります。

ループの形は自由に設定できます。めちゃくちゃな形でもかまいません。比例定数は 1 です。比例定数が 1 ということは、これはたまたま 1 になったということではなく、電流の大きさを定義したあと、この法則によって磁場の大きさを定義したということです。（さらにそのあとWbを定義したということです）。この法則の考え方はガウスの法則に似ています。

この法則をちゃんと書き直すと、

1Wb の磁極が、任意の閉曲線に沿って１周するとき、磁場がその磁極にする仕事は、閉曲線の内部を貫く電流の大きさに等しい、

となります。

これをアンペールの法則といいます＊19世紀のフランスの物理学者アンドレ＝マリ・アンペールが発見しました。右ねじの法則はアンペールの法則の一部です。電流の単位 アンペア もこの人にちなんでいます。
　閉じる。磁場が 1Wb の磁極にする仕事、というのは、磁場の中の単位磁荷を動かすためのエネルギーのことです。『電位』項を参照してください。この法則についての詳細は大学で学びます。

ビオ・サバールの法則

電流と磁場の関係を微小部分に分解して考えたものが、ビオ・サバールの法則です＊19世紀のフランスの物理学者ジャン＝バティスト・ビオ、同じく19世紀のフランスの物理学者フェリックス・サバールの二人によって発見されました。
アンペールも、ビオも、サバールも、同じ時期の同じ国の人です。
　閉じる。

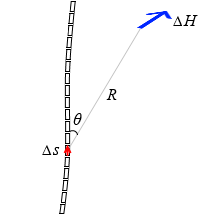I [A] の電流を微小部分 Δs [m] に分解し、その微小部分の電流が、R [m] だけ離れた位置につくる磁場の強さ ΔH [A/m] は、Δs と とのなす角を θ とすると、

  ΔH = \(\large{\frac{1}{4\pi}}\)⋅\(\large{\frac{I\cdot \Delta s\cdot\sin\theta}{R^2}}\)

という式で表される関係になっています。

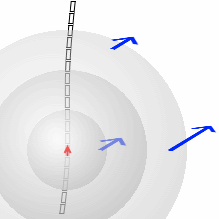微小部分の電流は、距離が離れるとその2乗に反比例して影響力が小さくなり、また、角度がついていても影響力が小さくなる、という法則です。

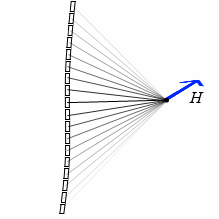この、微小部分の電流がつくる微小な磁場を、無数に足し合わせて（積分して）いったものがその地点の磁場です。

このビオ・サバールの法則は本質的にはアンペールの法則と同じものなのですが、これ以上詳しいことは大学で学びます。

直線電流がつくる磁場の式の導出

アンペールの法則による導出

まず、アンペールの法則を使って導き出してみます。

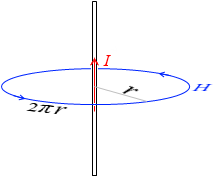
I [A] の直線電流を中心とする半径 r [m] の円周に沿って 1Wb の磁極を１周させるときの仕事を考えます。

直線電流から r だけ離れた位置の磁場の強さを H とおきます。すると自動的に、半径 r の円周を周回している最中の磁極にはたらく磁場の強さは H となります。周回の途中で 1.2H になったり、0.8H になったりすることはありません。ずっと H で一定です。

このように、アンペールの法則というのは、どの場所でどのくらいの磁場の強さであるかが分かっているときに適用する法則です。そして今回は、円の形の経路を進めば磁場の強さの値が一定である、ということを利用します。「円」の経路上であれば磁場の強さが特定できています。（そうでない経路だと磁場の強さが不明です）

周回するときの磁場の強さは本当に一定なのか、1.2H になったり、0.8H になったりしないのか、とツッコミたくなるかもしれませんが、実験では一定になっているし、電流の影響はきれいに放射状に広がっていると予想され、まあ一定ということで間違いないだろう、としかいえません。

この円周上で 1wb の磁極を動かすための力 F は

　　　　F = mH = 1×H = H

です。力の向きは円周の向き（接線の向き）です。これを円周 2πr の距離だけ動かすのだからその仕事は、

（仕事＝力×距離）= H × 2πr

で＊よくわからないという方は 『重力による位置エネルギー』項や『電位』項を参照してください。
　閉じる、アンペールの法則によれば、これが電流 I に等しいのだから、

　　　　I = H × 2πr

　　∴　H = \(\large{\frac{I}{2\pi r}}\)

となり、直線電流がつくる磁場の式が導き出せました。

ビオ・サバールの法則による導出

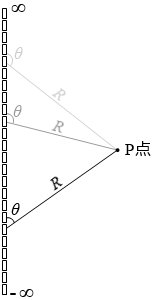ビオ・サバールの法則によって導き出すときの考え方は、微小部分の電流による微小な磁場を、無限の長さの分、足し合わせるというものです。

これは、ビオ・サバールの法則の式

　　　　ΔH = \(\large{\frac{1}{4\pi}}\)⋅\(\large{\frac{I\cdot \Delta s\cdot\sin\theta}{R^2}}\)

を -∞ から ∞ まで積分するということです。θ や、微小部分からP点までの距離 R が刻々と変化するのを積分するのです。

一応、式を書くだけ書いてみます。高校生は覚える必要はありません。大学の教科書に詳しく載ってます。

　　　　H = \(\large{\frac{1}{4\pi}}{\Large \int}_{-\infty}^{\infty} \frac{I\sin\theta}{R^2} \small{ds}\) = \(\large{\frac{I}{4\pi}}{\Large \int}_{0}^{\pi} \frac{\sin\theta}{r} \small{d\theta}\) = \(\large{\frac{I}{4\pi r}}\bigl[\small{-\cos\theta} \Bigr]^\pi_0\) = \(\large{\frac{I}{4\pi r}}\Bigl((\small{-(-1)}\large{)}-(\small{-(1)}\large{)}\Bigr)\) = \(\large{\frac{I}{2\pi r}}\)

円形電流がつくる磁場の式の導出

アンペールの法則による導出

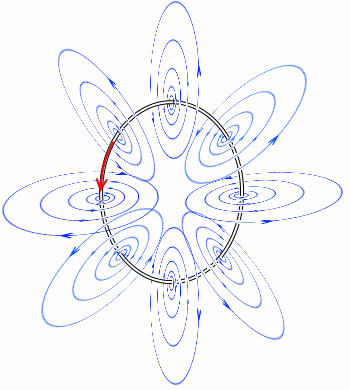円形電流がつくる磁界をアンペールの法則を使って導出するのは難しいです。電流をとりまく磁力線の円が少し外側により、磁場がどうなっているのかよく分かりません。アンペールの法則を適用するための経路が分かりません。絶対無理というわけではないのですが、筆者には分かりません。

アンペールの法則を使うときというのは、円とか長方形などといったような単純な経路に沿って磁極を動かすときで、さらにそのとき磁極にはたらく磁場が明確になっているときです。

ビオ・サバールの法則による導出

というわけで、円形電流がつくる磁場の式を求めるときはビオ・サバールの法則を使います。

直線電流がつくる磁場のときと比べると、

無限の直線を、短く切って（半径 r の約6.28倍に＊6.28 ≒ 2π閉じる）、丸めた場合の磁場、といえます。

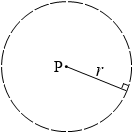各微小部分と中心点Pとの距離は r です。各微小部分とP点との角度は 90° です。

つまり、ビオ・サバールの法則の式

　　ΔH = \(\large{\frac{1}{4\pi}}\)⋅\(\large{\frac{I\cdot \Delta s\cdot\sin\theta}{R^2}}\)

の分母の R が r で、分子の θ が 90° つまり sinθ = 1 です。

すなわち、

　　　　ΔH = \(\large{\frac{1}{4\pi}}\)⋅\(\large{\frac{I\cdot \Delta s\cdot1}{r^2}}\)

　　　　　　= \(\large{\frac{I}{4\pi r^2}}\)⋅Δs

これが、一つの微小部分がP点につくる微小磁場です。そして、これはどの微小部分においても同じです。

ですので、これを一周分積分したいのですが、これは単純に、\(\large{\frac{I}{4\pi r^2}}\) に一周分の長さ 2πr を掛ければいいわけです。

Δs を一周分積分すると、\({\large \int}_{0}^{2\pi r} \small{ds}\) = 2πr であるということです。＊2πr を 1万個に分割したものが Δs なら Δs を 1万回足し合わせるし、2πr を 1億個に分割したものが Δs なら Δs を 1億回足し合わせるし、結局積分すると 2πr になる、ということです。
　閉じる

つまり、P点の磁場の強さは、

　　　　H = \(\large{\frac{I}{4\pi r^2}}\)⋅2πr

　　　　　= \(\large{\frac{I}{2r}}\)

です。

（ΔH：微小磁場、H：総計磁場）

ソレノイドがつくる磁場の式の導出

アンペールの法則による導出

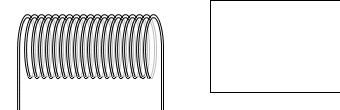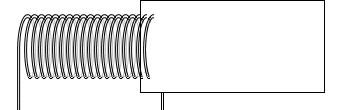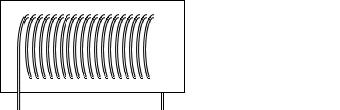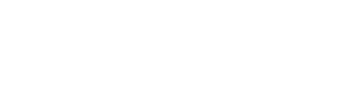ソレノイドの断面を図示すると、

このようになります。

は紙面の向こう側からこちら側、 は紙面こちら側から向こう側、ということを示しています。

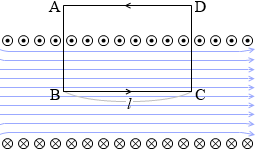ソレノイド内部の磁場を H 、1m当たりの巻き数を n とし、左図のような長方形の経路A→B→C→D→A（BCの長さ l )を考えます。

経路A→Bでは磁力線と垂直なので 1Wb の磁極は磁場から力を受けずに移動することができ＊『電位』項参照。閉じる、その仕事は 0 。
経路B→Cでは磁力線にそって進み、そのときの力が 1×H で距離が l だから仕事は Hl 。
経路C→Dでは磁力線と垂直なので仕事は 0 。
経路D→Aでは（ソレノイドの外側には磁場が無いので）仕事が 0 。

よって、

（A→B→C→D→Aの仕事）= 0 + Hl + 0 + 0 = Hl

となります。そして、この経路に取り囲まれる電流の総計は I × n × l ＊ ABCDに囲まれる導線の本数は n × l 本。 のことです。上のイラストでは8本。
1本当たりの電流は I だから、電流の総計は I × n × l 。
　閉じるだから、アンペールの法則により、

　　　　Hl = Inl

　　∴　H = nI

と求められます。

ソレノイド内の磁場は一様

次に、ソレノイド内の磁場が一様であることを説明します。

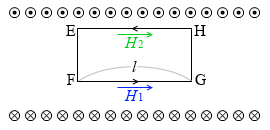左図のような長方形の経路E→F→G→H→Eを考えますと、
経路E→Fの仕事が 0 、
経路F→Gの仕事が H₁l 、
経路G→Hの仕事が 0 、
経路H→Eの仕事が - H₂l 、

この経路が取り囲む電流が 0 だから、

　　　　0 + H₁l + 0 - H₂l = 0

　　∴　H₁l = H₂l

　　∴　H₁ = H₂

となり、H₁ の磁場と H₂ の磁場が等しいことが分かります。ソレノイド内ではどのような長方形を考えても、このことが成り立っていますので、ソレノイド内の磁場はあらゆる地点で等しい、つまり一様であるといえます。（ただし出口付近、入り口付近は磁力線が曲がっているでしょうから一様とはいえません）

円形電流の場合は一様ではない

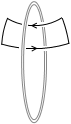円形電流の場合は、磁場が一定となるようなラインをたどると左図のような経路が考えられますが、これでは磁場が平行ではなく、一様とはいえません。

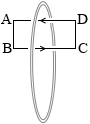長方形の経路を考えると、確かに、

　　(A→B)+(B→C)+(C→D)+(D→A) = 0

が成り立ってはいるのですが、(A→B) = (C→D) ではないし、(B→C) = (D→A) でもなく、磁場が平行とはいえず、一様とはいえません。（４辺の合計は 0 になるが、２つずつ等しくなっているわけではない）

ビオ・サバールの法則による導出

ソレノイドがつくる磁場をビオ・サバールの法則から導き出すのはちょっと面倒なので、その説明は割愛させてください。大学の教科書には載ってると思います。

円形電流のときは、アンペールの法則よりもビオ・サバールの法則の方が適用が楽でしたが、ソレノイドの場合はビオ・サバールの法則よりもアンペールの法則の方が適用が楽です。

ソレノイドの磁場が半径によらないことの説明

ソレノイドがつくる磁場の式　H = nI　には半径 r の文字が含まれていないので、半径が大きかろうが小さかろうが磁場の強さは変わらないということですが、

これは、半径が大きくなればその分、電流の微小部分の個数が増えるので、磁場が小さくならないということです。半径が大きくなると、たとえば中央付近は電流からの距離が遠くなるので磁場の強さが小さくなると思いがちですが、その分、中央付近に影響を与える微小部分の個数が増えるのでトータルで変わらないのです。

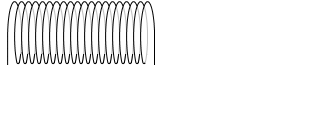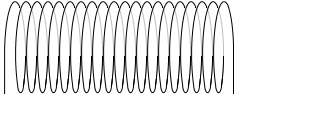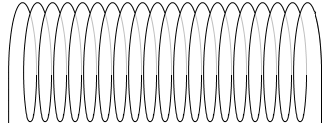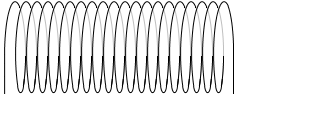もし、半径が大きくなったときに、1m当たりの巻き数 n も小さくなってしまうようなら、磁場も小さくなってしまいますが、

（左図は、半径が大きくなると同時に n も小さくなっている）

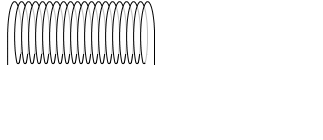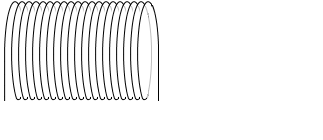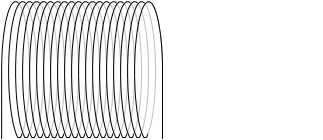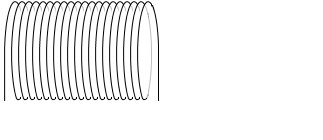半径が大きくなったときに、1m当たりの巻き数 n が変わらないのであれば、磁場も変わりません。

（左図は、半径が大きくなるときに n が変化していない）

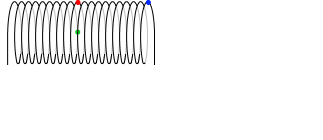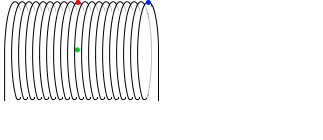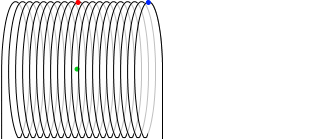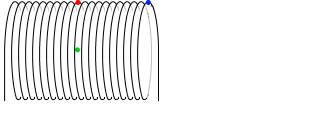赤点の微小部分が緑点に与える影響は小さくなりますが、青点の微小部分が緑点に与える影響は大きくなります。上で示したビオ・サバールの法則の式の sinθ が大きくなるからです。

対して、円形電流のときは、磁場は、導線付近では強く、中央付近では弱いので、半径が大きくなれば、その分、中央付近の磁場は弱くなってしまいます。（上のイラストでいうところの青点のような微小部分が無い）。ですので円形電流の磁場の式　H = 　の分母には r が現れます。