仕事
物体に一定の力 F [N] を加え続けて、その力の向きに距離 s [m] ＊なぜ量記号に s を用いるかわかりません。
閉じるだけ動かしたとき、その積 F × s を、力が物体にした仕事といいます。この「仕事」というのは物理用語です。日常会話で使う「仕事」とは違います。量記号に W を用います＊work（仕事）から。もしかすると James Watt からかもしれません。
大文字を使います。小文字は使ってはいけないらしいです。
量記号の W と、単位のワット [W] を混同しないように気をつけてください。
閉じる。
仕事の単位は、力[N] × 距離[m] ですから [N・m] ですが、これをたいてい [J]（ジュール＊19世紀のイギリスの物理学者ジェームズ・プレスコット・ジュールから。
この単位は物理のあらゆる分野で登場してきます。
『ジュール熱』、『熱の仕事当量』参照。
閉じる）で表します。[N・m] = [J] です。エネルギーと同じ単位です。エネルギーは仕事に変換できます。
この仕事というのは、最初の一瞬だけ力を加えるのではありません。ずっと力を加え続けるのです。
そしてその力は「ゆっくり」動くような力の加え方をすることが多いです。なぜゆっくりでなければならないかについては、補足ページをご覧ください。
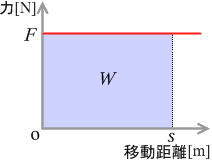縦軸に力 F 、横軸に移動距離 s をとったグラフを描くと、その面積部分が仕事 W の大きさになります。
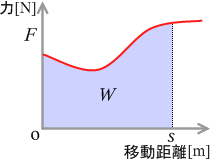もし加える力が一定でない場合は、左図のような面積部分が仕事の大きさとなります。
ここで不思議に思うことがあるかもしれません。仕事とは力×距離である、ということは、力を加えても移動しなければ仕事をしたことにならないのか、ということです。たとえば重い物を手で持っているとき、物は動いてなくても筋肉には力が入っていますし、エネルギーを消費しています。このような場合はどう考えるかというと、使ったエネルギーは、手や腕を構成する細胞を温めただけで、物体には仕事をしていないと考えます。人間はカロリーを消費して手と腕とその周りの空気の温度を上昇させましたが、物体には仕事をしていないのです。＊
カロリーを消費するというのは筋肉を収縮させるということであり、筋肉を収縮させるということは筋肉に電気を流すということです。人間が疲れるのは電気エネルギーを使ったからです。電気エネルギーを使わないように、たとえば頭の上に物を載せてうまくバランスを取れば人間は疲れません。
椅子に座ったときなどに頬杖をつくのはなるべく筋肉を使わないようにするためです。
骨で物を支えれば電気エネルギーを消費しません。温度も上がりません。筋肉で物を支えると電気エネルギーを消費します。温度が上がります。
閉じる
「手が物体にした仕事」というのは、どのくらいの力を入れて、その状態でどのくらいの距離、移動したのかを表す量です。手の温度が上がった度合いはカウントしません。
力の向きと移動の向きが異なるときの仕事
上記の公式 W = F s は、「その力の向きに距離 s だけ動かしたとき」の仕事を表すものです。ですから、力の向きと移動の向きが異なる場合は、力を分解して、移動に関わる成分だけを適用しなければなりません。
例えばレールの上しか移動できない物体に、それとは異なる向きの力を加えて動かすとき、
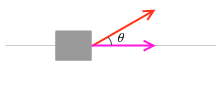物体になされた仕事に適用する力は、Fcosθ です。
ですので、力の向きと移動の向きが異なる場合も考慮すると上記の仕事の公式は次のようになります。（ただし、θ のとり方が違うと、下記の cosθ は sinθ となります。要は力を分解した２つのうちの、移動と同じ向きの方ということです。）
向きが違う例
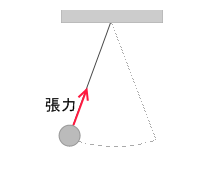たとえば振り子の糸の張力（向心力）は、振り子の球の運動方向と常に直角＊円の中心から下ろした垂線は接線と直交するという定理を思い出してください。
『運動方向と運動方向と垂直な方向に分解』もご参照ください。
閉じるなので F cosθ = F cos90°= 0 であり、仕事は W = F s cosθ = 0 です。糸は球に対して仕事をしないのです。
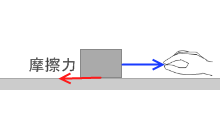あらい面上の物体を手でゆっくり引っ張る（＝摩擦力と等しい力で引っ張る）とき、手が物体にする仕事は F s ですが、摩擦力が物体にする仕事は - F s です。摩擦力と物体の移動の向きは逆なので、cosθ = cos180°= -1 だからです。摩擦力が物体にした仕事 W は F s cosθ = - F s です。負です。
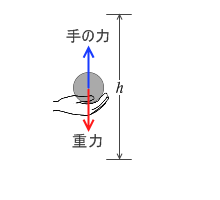質量 m の球を手の力で高さ h までゆっくり持ち上げる（＝重力と等しい力で持ち上げる）場合、手の力は重力 mg と同じ大きさなので、手が球にする仕事は mgh です（ F ⇒ mg 、s ⇒ h ）。（『重力による位置エネルギー』参照）。重力の向きは球の移動の向きと逆なので、重力が球にする仕事は - mgh です。
逆に、高い位置から手で支えながらゆっくり下ろす場合は、手が球にする仕事が - mgh で、重力が球にする仕事が mgh です。
さらに、高い位置から手を触れずにストンと球を落とす場合、重力が球にする仕事は mgh です。（補足ページ「ゆっくり」の例外参照）。手が球にする仕事は 0 です。触ってないのですから。