ケプラーの法則
惑星の運動
中世までは宇宙の中心は地球であり、天体は地球を中心として動いているという天動説（天が動く）が主流の考えでした。
16世紀のコペルニクス以降は太陽を中心としてその周りを惑星が回るという地動説（地球が動く）が主流になっていきました。
17世紀初頭、ドイツのケプラーは、太陽系の惑星＊太陽系の惑星というのは太陽の周りを回る、水星、金星、地球、火星、木星、土星、天王星、海王星の８つの惑星のことです。冥王星を加えて９つとすることもあります。
閉じるの精密な観測結果を分析し、下で説明する３つの法則を発見しました。
そしてケプラーの法則の発見が物理学の根幹となる万有引力の法則の発見へとつながっていきます。
ケプラーの第１法則
惑星は太陽を１つの焦点とする楕円軌道を描く。
楕円というものには焦点が２つあるはずですが、実際には、太陽ではないもう一方の焦点の位置には特に何も存在しません。あと、楕円といっても実際には円に近い楕円になっています。
我々が普段日常生活で目撃する回転運動は楕円ではなく円が多いです。中心との距離が固定されている運動です。しかし万有引力の世界では楕円軌道が普通です。中心との距離が固定されておらず、力が距離の2乗に逆比例する場合の運動です。
なぜ楕円になるかについては高校物理では導き出せません。大学で学びます。
万有引力の法則の式を解いて軌道の式を割り出すと、円錐曲線の式が出てきます。円錐曲線というのは楕円、放物線、双曲線のことで、万有引力によって運動する物体はこれらのうちどれかの軌道を描くのですが、放物線、双曲線を描くような物体は太陽系の外に飛び出していってしまうので現存せず、惑星として残っているものは楕円軌道を描いています。円は楕円の一種なのですが、現存する惑星は円に近い楕円軌道を描いています。長軸が短軸に比べて長い楕円（細長い楕円）軌道を描くような物体は他の物体と衝突しやすく、合体してしまうので残らず、円に近い楕円軌道を描く物体だけが残り、それが水金地火木土天海の８つの惑星となっています。
概略はこんな感じですが興味のある人は「ケプラーの法則 導出」などのキーワードで検索してみてください。
ケプラーの第２法則
惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である。
この法則は面積速度一定の法則ともいいます。
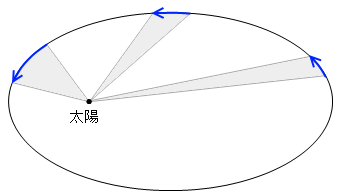周回する物体と焦点とを結ぶ線分を動径といいますが、この動径が単位時間当たりに掃く（描く）面積が一定ということです。この面積が一定ということは、惑星は太陽に近いときは速い速度で、遠いときは遅い速度で動くということです。＊実際の惑星の軌道は左図のような楕円ではなく、円に近い楕円です。
閉じる
これは角運動量保存の法則というものを表しています。大学で学びます。中心力以外の力がはたらかない場合、回転の勢いは保存される、という法則です。力のモーメントから類推してもらうと分かると思いますが、回転の勢いは、距離が遠いほど強い（中心軸を回転させる力が強い）といえますので、それを一定に保つためには距離が遠いときほど小さく動き、距離が近いときほど大きく動く必要があります。このような動き方をすれば、回転の勢いは一定であるといえます。
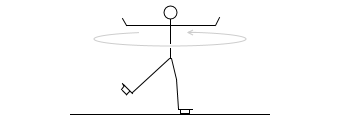フィギュアスケーターがスピンをするとき、伸ばしていた手足を縮めると回転スピードが上がります。角運動量保存の法則がはたらいているからです。このときも面積速度は一定です。
面積速度を数式で表してみます。
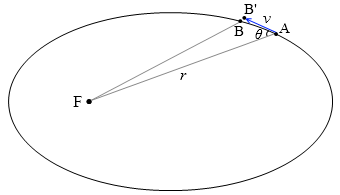
A点にいた惑星が v の速さで単位時間にB点に進んだとします。AB間が微小な場合はFABの面積は三角形FAB'に近似できます。動径 r と速度 とのなす角を θ とすると、三角形FAB'は底辺 r 、高さ vsinθ の三角形でありますので、その面積 S は
S = \(\large{\frac{1}{2}}\)rvsinθ
と表せます。この S の値が一定なわけです。r が小さいときは v が大きく、r が大きいときは v が小さいのです。
そしてこの式に 2m（mは質量）を掛けると mrvsinθ となり、これは角運動量を表しています。（これは覚えなくていいです。大学の範囲です。）
ケプラーの第３法則
惑星の公転周期 T の2乗は、楕円軌道の半長軸 a の3乗に比例する。
これを数式で表すときは、
T2 = ka3 または \(\large{\frac{T^2}{a^3}}\) = k
と表現します。太陽からの距離が遠い惑星ほど一周するのに時間がかかります。（上のケプラーの第２法則は１つの惑星に着目したときの話で、このケプラーの第３法則は複数の惑星を比べたときの話です。）
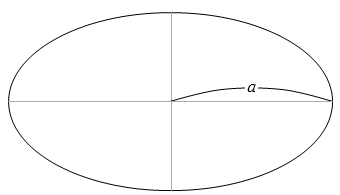半長軸というのは左図の a の部分のことです。
定数 k の値は太陽系の惑星ではすべて同じ値です。
太陽系外の恒星の惑星では違う値になります＊ところで、恒星と惑星の違いをはっきり認識してますでしょうか。恒星は自ら光っている大きい天体のことです。惑星は恒星の周りを回る光っていない天体のことです。太陽系というのは、太陽（恒星）とその周りの８つの惑星のことをいいます。
閉じる。恒星の質量が大きいほど公転周期は短くなります。
この法則も万有引力の法則から導き出されます。興味のある人は「ケプラーの第３法則 導出」などのキーワードで検索してみてください。