万有引力の法則
ニュートンが発見
ニュートン＊かの有名なアイザック・ニュートンのことです。1642年～1727年、イギリス。物理学の祖といえる人です。
閉じるは、惑星が太陽のまわりを回り続けるのは、惑星と太陽との間に引力がはたらくため＊引力が無ければ２つの物体は離れ離れになってしまいます。
閉じると考えました。そしてその引力の大きさは、ケプラーの法則から、惑星と太陽の距離の2乗に反比例し、惑星の質量＊厳密には、惑星と太陽の質量、に比例なのですが、今は太陽系の惑星のことだけを考えているので太陽の質量は省略します。
閉じるに比例するということを導き出しました。さらに、この力は、惑星と太陽との間にだけにはたらくのではなく、あらゆる万物の間にはたらくと考えました。これを万有引力の法則といいます。
ケプラーの法則から導き出す
惑星と太陽との間にはたらく引力の大きさを導き出してみます。
計算を簡単にするため惑星は楕円運動ではなく円運動をしていると仮定します。実際に太陽系の惑星の軌道は円に近い楕円になっています。
そうしますと、ケプラーの第２法則より、この円運動は等速円運動ということになり、『円運動』項や『向心力』項で学んだ各式が使えることになります。
求める引力を F 、惑星の質量を m 、円軌道の半径（惑星と太陽との距離）を r 、角速度を ω 、回転周期を T とします。
この引力は円運動する惑星にはたらく向心力のことだから、
F = mrω2 ω = \(\large{\frac{2\pi}{T}}\)を代入して、
= mr\(\bigl(\large{\frac{2\pi}{T}})\small{^2}\)
= \(\large{\frac{4\pi^2mr}{T^2}}\) ……①
次に、ケプラーの第３法則より、
\(\large{\frac{T^2}{a^3}}\) = k (kは定数)
今の場合、楕円を円とみなしているから、半長軸 = 半短軸 = 半径 、つまり a = r 、よって、
\(\large{\frac{T^2}{r^3}}\) = k
∴ \(\large{\frac{T^2}{r}}\) = kr2
∴ \(\large{\frac{r}{T^2}}\) = \(\large{\frac{1}{k\ r^2}}\)
これを上の①式に代入しますと、
F = \(\large{\frac{4\pi^2m}{k\ r^2}}\)
ここで \(\large{\frac{4\pi^2}{k}}\) を K とおきます。π も k も定数だから K も定数です。そうしますと、
F = K\(\large{\frac{m}{r^2}}\)
となります。
この式は、
惑星にはたらく引力の大きさは、惑星の質量に比例し、太陽からの距離の2乗に反比例する、 ……②
ということを表しています。
太陽側の立場も考慮
上で求めた式は惑星にとっての引力ですが作用⋅反作用の法則によれば太陽にも同じ大きさの力がはたらいているはずです。上式が惑星以外にも適用できるとするとそれは太陽にも適用できるということで、そうしますと、
太陽にはたらく引力の大きさは、太陽の質量に比例し、惑星からの距離の2乗に反比例する、 ……③
ということになります。
②と③を同時に満たすためには、
太陽と惑星の間にはたらく引力は、太陽の質量に比例し、惑星の質量にも比例し、太陽と惑星との距離の 2乗に反比例する、
とならなければなりません。このことを式で表すと（太陽の質量を M 、定数を G とします）、
F = G\(\large{\frac{Mm}{r^2}}\)
となります。分子は M+m ではありません。これだと「太陽の質量に比例」かつ「惑星の質量に比例」となりません。M+m だとすると、M が2倍になったときに M+m は2倍になりません。足し算ではだめです。掛け算です。
万有引力の法則
ニュートンはこの力が惑星と太陽の間にだけはたらくのではなく、あらゆる物体間にはたらくと考えました。これを万有引力の法則といい、定数 G を万有引力定数といいます。小文字の g は重力加速度で、大文字の G は万有引力定数です。＊gravity より閉じる
万有引力定数
18世紀のイギリスの物理学者キャヴェンディッシュ＊ニュートンと同じトリニティ・カレッジ出身。
閉じるは、ねじり天秤を用いた実験で地球の比重を導き出しました。そしてその値から万有引力定数が導き出され、それは現在の高精度実験によると、
G = 6.67×10-11 N⋅m2/kg2
となっています。＊この数値はちょっと面白く、発表する機関によって数値がまちまちです。発表する年によっても違います。物理の根幹をなす数値なのに困ったものです。測定するのが難しいようです。測定が難しいほど小さい値だともいえます。
閉じる
斥力は無い
静電気力（クーロン力）には引力と斥力がありますが、万有引力には引力しかありません。斥力はありません。
重力
重力＝万有引力
重力加速度を g とすると質量 m の物体にはたらく重力は mg であることはお分かりだと思います。そして、この重力が万有引力のことであるということを『慣性質量と重力質量』で少し説明しました。ここでもうちょっと詳しく説明します。
全質量が地球の中心に凝縮されているとみなす
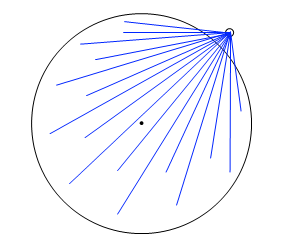ある物体が地球表面付近にあるとき、その物体と地球との万有引力がその物体にはたらく重力であるわけですが、厳密にいうと、地球を無数の小片に分割したときにそれら一つひとつと物体と間の万有引力の総和が重力であるわけです。しかし数学の積分によりますと、球体の各質点との間の引力の総和は球体の中心に全質量が集まったときの引力と等しいことが示されます。ここでは説明できません。数学の本を見てください。
遠心力を無視する
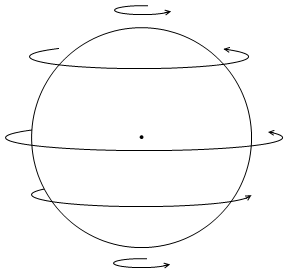地球は自転していますので、地表にくっついている物体には遠心力がはたらきます。
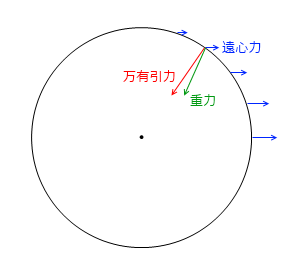北極点、南極点で遠心力は 0 になり、赤道で最大になります。万有引力と遠心力のベクトル和が重力となるわけです。ですので重力は厳密にいうと赤道付近ではわずかに小さくなっています。
しかし遠心力は万有引力に比べて小さい＊遠心力が最も大きくなる赤道上でも約 1/300 です。
閉じるのでここでは無視します。
高さを無視する
万有引力の大きさは距離によって変わるので、物体を足元に置いたときと頭の上に置いたときでは地球との距離が変わってくるはずですが、地球の半径に比べたらとても小さいので無視します。富士山の高さ 3.776×103m と地球の半径 6.4×106m を比べてもだいたい 1:2000 です。
関係式
というわけで、地表付近の質量 m の物体にはたらく重力は、6.4×106m （これを R とおきます）だけ離れた位置にある質量 M （地球の質量）の物体との間の万有引力であるから、
mg = G\(\large{\frac{Mm}{R^2}}\)
であります。すなわち、
g = \(\large{\frac{GM}{R^2}}\) または GM = gR2
この式から地球の質量 M を求めてみます。以下の３つの値を代入して M を求めます。
g = 9.8 m/s2
R = 6.4×106 m
G = 6.7×10-11 N⋅m2/kg2 = 6.7×10-11 (kg⋅m/s2)⋅m2/kg2 = 6.7×10-11 m3/kg⋅s2 ＊
N = (kg⋅m/s2) となるのはお分かりでしょうか。
運動方程式 ma = F より、
(kg)⋅(m/s2) = N
です。
（単位の演算 参照）
閉じる
そうしますと、
M = \(\large{\frac{g\ R^2}{G}}\) = \(\large{\frac{9.8\ \times\ (6.4\times10^6)^2}{6.7\times10^{-11}}}\) = \(\large{\frac{9.8\ \times\ (6.4^2\times10^{12})}{6.7\times10^{-11}}}\) = \(\large{\frac{9.8\ \times\ 6.4^2}{6.7}}\)×1023 ≒ 59.9×1023 ≒ 6.0×1024 kg ＊
単位について
\(\large{\frac{g\ R^2}{G}}\) = \(\large{\rm{\frac{m/s^2\ \times\ m^2}{m^3/kg\cdot s^2}}}\) = \(\large{\rm{\frac{m^3/s^2}{m^3/kg\cdot s^2}}}\) = \(\large{\rm{\frac{1}{1/kg}}}\) = kg
閉じる
何トンでしょうか。大きすぎてよく分かりません。
重力における反作用は無視
地表に置かれた物体には重力が掛かって地球に引っ張られているわけですが、実はこのとき地球も物体に同じ大きさで引っ張られています＊これは垂直抗力とは違います。『つり合いと作用⋅反作用の区別』項の『他の例』の説明をよく読んでください。
閉じる。しかし地球の重さに比べると微々たるものなので今まで無視してきたわけです。
たとえば、物体が数メートルの高さから落とされたとき、重力によって物体は下に落ちていきますが、同時に地球は上にごくわずかに引き上げられているのです。あまりにもごくわずかなので無視しているのです。
重力加速度の値
重力加速度の値は、物体を自由落下させたり、振り子を振ったりして測定します。厳密な測定は真空中で行うようです（国土地理院参照）。その値は測定場所や季節によって変動しますが、国際的に g = 9.80665 m/s2 と定められています。高校物理ではたいてい g = 9.8 m/s2 です。
mg = G\(\large{\frac{\textcolor{#c0c}{M}m}{\textcolor{#c0c}{R^2}}}\) = 9.8m
です。
言葉の定義
普通、重力加速度といったら地球表面での重力加速度のことです。しかし、月の表面での重力加速度というものも考えられるだろうし、人工衛星の重力加速度というものも考えられます。
重力という言葉も、普通は地球表面での重力のことをいいます。高校物理で「質量 m の物体に掛かる重力は mg である」といった場合には、これは地球表面での話です。しかし、月の表面での重力というものも考えられますし、ある物体とある物体の間の重力というものも考えられますし、重力と万有引力は同じものであるので、ある物体とある物体の間の万有引力ということもあります。しかし、地球表面での重力というものを厳密に考えて、地球の遠心力も含めて考えるとすると、万有引力と遠心力の合力が重力ということになり、万有引力と重力は違うものということになります。「地球表面での重力」と「万有引力」という２つの言葉を別物として使い分ければスッキリするのですが、宇宙論などの分野では万有引力のことを重力と呼んだりしていて、どうにもこうにもややこしいです。
月の重力
地球表面での重力と月表面での重力の大きさを比べてみます。
地球表面での重力を
mg = G\(\large{\frac{Mm}{R^2}}\)
としますと、月表面においては、
月の質量が地球に比べて\(\large{\frac{1}{80}}\)弱 \(\large{\frac{7.348\times10^{22}\ \rm{kg}}{5.972\times10^{24}\ \rm{kg}}}\)M ≒ 0.0123×M
月の半径が地球に比べて\(\large{\frac{1}{4}}\)強 \(\large{\frac{1737\ \rm{km}}{6371\ \rm{km}}}\)R ≒ 0.2726×R
なので、
mg月 ≒ G\(\large{\frac{0.0123Mm}{(0.2726R)^2}}\) ≒ 0.1655×G\(\large{\frac{Mm}{R^2}}\)
です。月表面での重力加速度は
g月 ≒ G\(\large{\frac{0.0123M}{(0.2726R)^2}}\) ≒ 0.1655×\(\large{\frac{GM}{R^2}}\) = 0.1655×9.8 ≒ 1.622
です。
よく「月の重力は地球の約\(\large{\frac{1}{6}}\)」といわれますが、これは 0.1655 のことです。
落下の速さ
1円玉の重さは1gですが、それと同じ重さの羽毛を用意して、２つを同じ高さから同時に落下させると、1円玉の方が早く地面に着地します。羽毛は1円玉より空気抵抗をたくさん受けるので落下の速さが遅いです。空気中の窒素分子や酸素分子が落下を妨害するのです。しかしこの実験を真空容器の中で行うと、1円玉と羽毛は同時に着地します。空気抵抗が無ければ同時に着地します。羽毛も1円玉と同じようにストンと勢い良く落下します。真空中では落下の速さは物体の形、大きさと無関係です。
真空容器の中で同じ実験を1円玉と10gの羽毛とで行ったとしても、２つは同時に着地します。落下の速さは重さとも無関係です。
万有引力の式 F = G\(\large{\frac{Mm}{r^2}}\) の m が大きくなれば万有引力 F も大きくなるのですが、同時に運動方程式 ma = F の m も大きくなるので a に変化は無いのです。万有引力が大きくなっても、動かしにくさも大きくなるので、トータルで変わらないのです。
上で示した関係式
mg = G\(\large{\frac{Mm}{R^2}}\)
の右辺の m が大きくなると同時に、左辺の m も大きくなるので、g の大きさに変化は無いということです。
つまり、空気抵抗が無ければ、落下の速さ（重力加速度）は物体の形、大きさ、質量に依らないのです。