摩擦力を受ける運動

摩擦力を受ける運動

摩擦力を受ける運動について考えてみます。

摩擦力には、静止摩擦力と動摩擦力がありましたが、静止摩擦力というのは物体が静止しているときの話なのでここでは関係ありません。『斜面上の運動』でも述べたように、静止しているときは加速度が 0 なのだから運動方程式が立てられませんし、静止しているとき問題になるのは力のつり合いの具合についてです。

ここで考えるのは、物体が動摩擦力を受けながら運動しているときの運動方程式や加速度についてです。

今、水平なあらい面の上に物体が置かれています。

右向きに力を加えて物体を動かします。物体が動くということはこの力は動摩擦力より大きいということです。この力は一瞬だけ加えるのではなく、物体が動いている最中も一定の力で加え続けます。物理の問題を解く上で注意しなければならないのは、力を一瞬だけ加えるのか、ずっと加え続けるのかということです。今はずっと加え続けます。

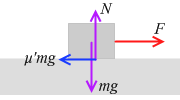物体の質量を m 、動摩擦係数を μ' 、加える力を F 、垂直抗力を N 、物体の加速度を a とします。

垂直抗力というのは押し付ける力のことですから、

　　　　N = mg

よって、動摩擦力は、

　　　　μ' × N = μ'mg

この力は物体の動きを妨害する方向にはたらきます。よって、物体に作用する合力は、（右向きを正として）

　　　　F - μ'mg

運動方程式を立てると、

　　　　ma = F - μ'mg

よって、加速度は、

　　　　a = \(\large{\frac{F}{m}}\) - μ'g

もし F = μ'mg であれば、a = 0 になります。加速度が 0 、つまり、物体は等速で運動します。＊たいていの場合、動摩擦力より最大静止摩擦力の方が大きいので、止まっている物体に F = μ'mg の力を加えても動き出しませんが。
　閉じる