斜面上の運動

斜面上の運動

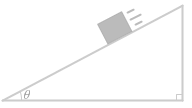水平面と θ の角度をなす斜面の上の質量 m の物体が滑り落ちる運動を考えます。

斜面は摩擦の無いなめらかな面であるとします。

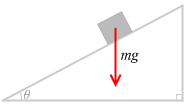物体には鉛直下向きに重力 mg がはたらいています。

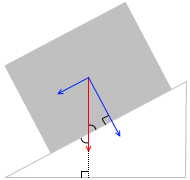
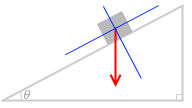この重力 mg を運動方向（斜面方向）と運動方向と垂直な方向に分解します。

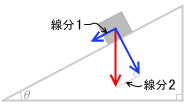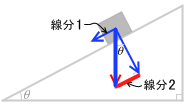運動方向の力の成分（左図の線分1）は、左図の線分2と同じであり、これを求めると、mgsinθ です。この力が物体を滑り落としています。

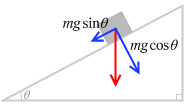運動方向と垂直な方向の力の成分は mgcosθ であり、この力は垂直抗力とつり合っています。つり合っているのでこの方向には物体は動かないので、今この方向に関しては何も考えません。

←（この図は演習問題で頻出です。確実に覚えてください。）

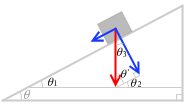ここで角の扱いに慣れていない方のために、左図の θ₃ が、なぜ θ になるか説明します。

最初に三角形の底辺（水平線）と平行な補助線を引きます。すると、 θ = θ₁ であり、 θ₁ = θ₂ であります。θ₂ というのは 90° - θ’ であり、θ₃ も 90° - θ’ である＊三角形の内角の和は 180° で、３つのうちの１つが 90° なのだから残りの２つの合計は 90° 。
　閉じるので、θ₂ = θ₃ であります。結局 θ = θ₃ となります。＊θ = θ₃ の証明方法は何通りかあります。
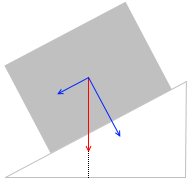例えば、mg に沿った鉛直な補助線を引きます。

すると対角の等しい2つの直角三角形ができ、

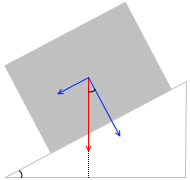θ = θ₃ とわかります。
　閉じる

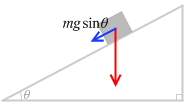
斜面方向の加速度を a （斜面下向きが正）として、運動方向の運動方程式を立てますと、

　　　　ma = mgsinθ

となり、加速度は、

　　　　a = gsinθ

となります。

運動方向と運動方向と垂直な方向に分解

物理の演習問題を解くとき、運動方向と運動方向と垂直な方向に分解することがよくあります。非常によくあります。このとき、運動方向と垂直な方向には物体は動いていないわけです。加速度が 0 ということです。つまり、運動方程式 ma = F の両辺が 0 になり、運動方程式の立てようがないのです。別のいい方をすれば、力がつり合っているということです。

物理の演習問題では、運動方程式を立てるか、つり合いの式を立てるか、が非常に多いです。

そして、よくある間違いが、運動方向と運動方向と垂直な方向に分解しなければいけないところを、水平方向と鉛直方向に分解してしまうことです＊運動方向と運動方向と垂直な方向を考えるだけでなく、それと合わせて、水平方向と鉛直方向も考えなければならない問題もありますが。
　閉じる。（垂直というのは何かに対して直角という意味で、鉛直というのは重力の方向という意味です。）

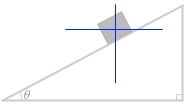　こうではなく、

　こうです。