コリオリ力

コリオリ力とは

コリオリ力（こりおりりょく）＊19世紀のフランスの物理学者、ガスパール＝ギュスターヴ・コリオリ。
　閉じるについて学ぶのは高校では物理の範囲でなく地学の範囲のようですが、これも慣性力の一種なのでここで説明しておきます。式の導出はせず、考え方だけ説明します。

地球規模で見たとき、北半球では風の軌道は右にカーブします。南半球では左にカーブします。

左回転しているメリーゴーランドの上でキャッチボールをするとボールは右に曲がってしまいます。右回転のメリーゴーランドでは左へ曲がります。

この、風やボールを曲げる力がコリオリ力です。この現象はフーコーの振り子（Wikipedia参照）という装置でよく実演されます。

コリオリ力は、回転座標と静止座標のずれによって引き起こされます。

いま、左回りに等速円運動する回転座標にA君とB君が乗っていて、A君がB君に向けてボールを投げたとします。

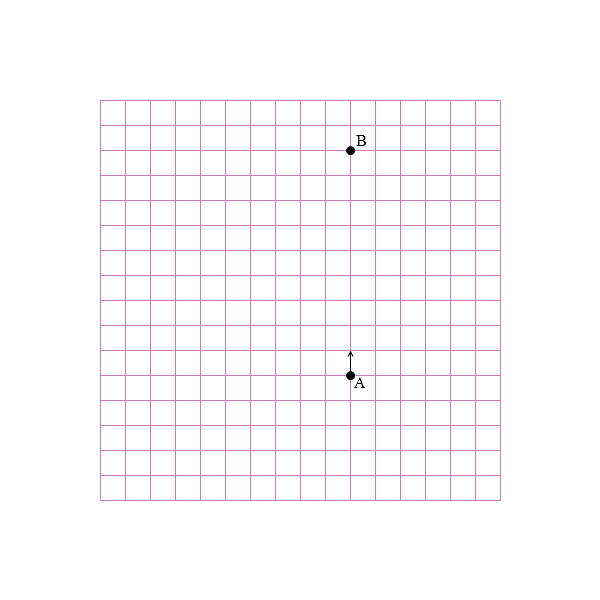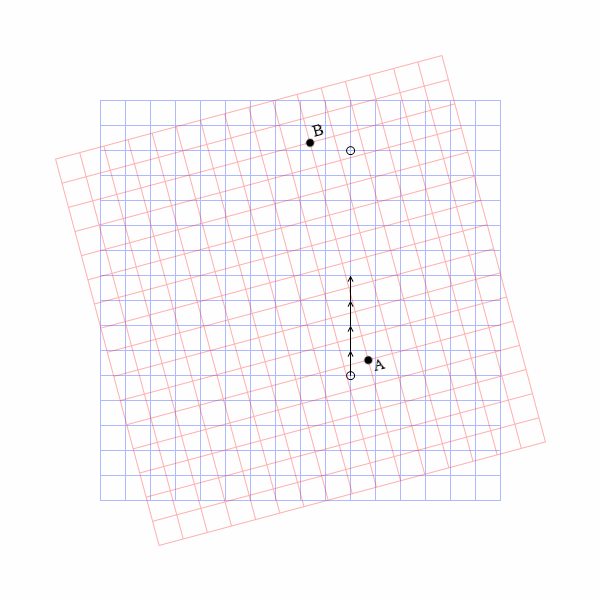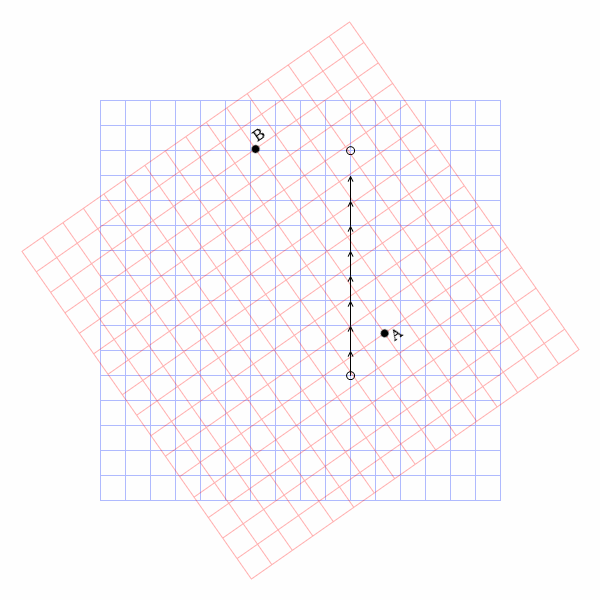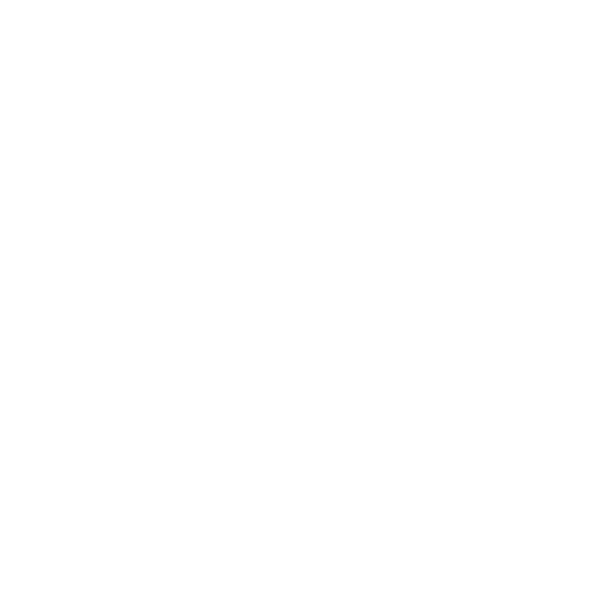
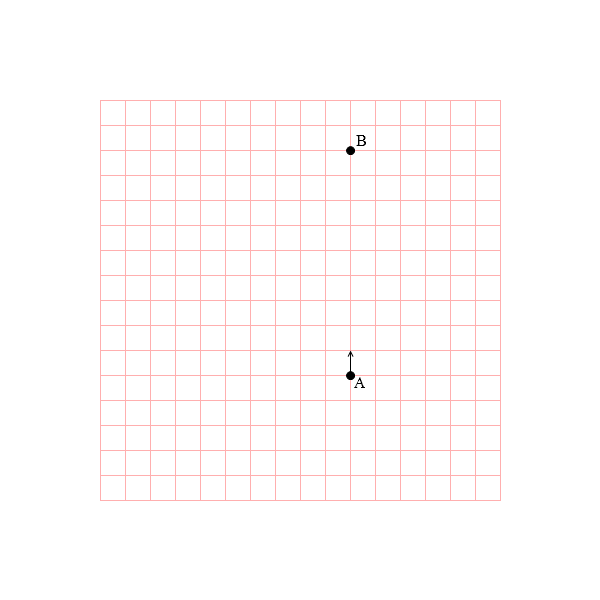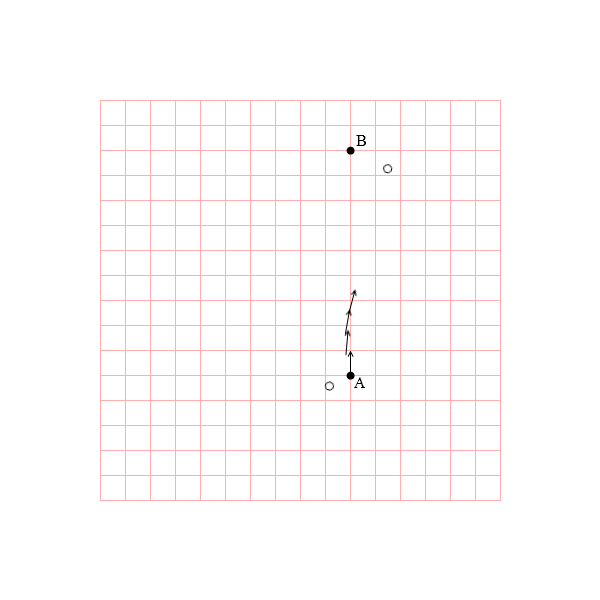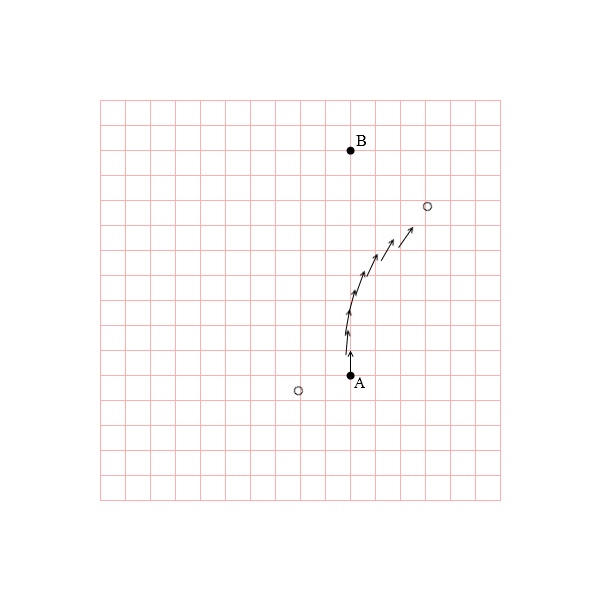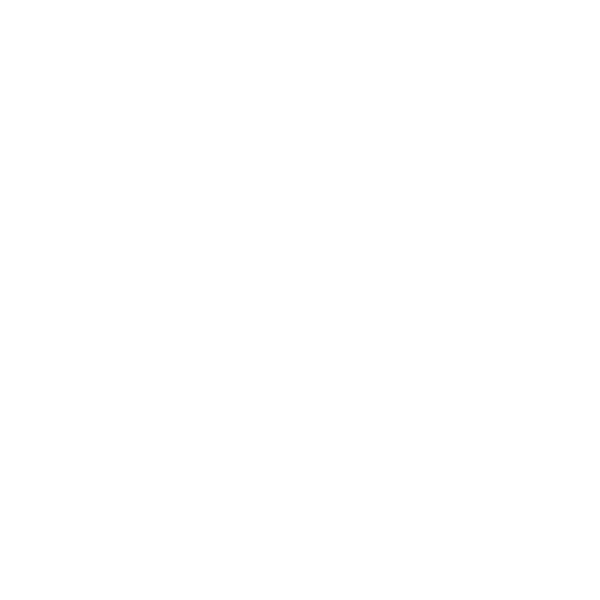
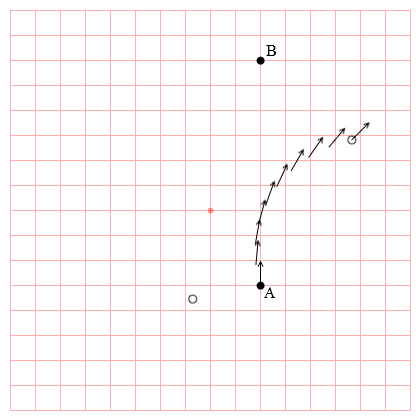
B君に向けて投げたボールは実際には見当違いの方向へ飛んでいってしまいます。

A君とB君は回転座標に結び付けられていますが、ボールはA君の手を離れた瞬間から回転座標の呪縛から逃れます。そのため、静止座標から見ればボールは真っ直ぐ飛びますが、回転座標から見るとボールは右へ曲がっていきます。これがA君とB君の感じるコリオリ力です。

このコリオリ力は回転座標のあらゆる地点で等しく作用します。B君がA君に向かって投げた場合もボールは右に曲がっていきます。回転の中心に近い位置でも遠い位置でもその効力の大きさは同じです。回転の中心の位置が別の場所にズレたとしても同じです。コリオリ力は物体の運動方向を変えるだけの力です。

回転座標が左に 3rad/s で回転していれば、ボールの進む向きは右に 3rad/s で変化しています＊回転座標が右に 3rad/s なら、ボールは左に 3rad/s です。
　閉じる。ボールがどの地点にいようと 3rad/s です。コリオリ力に関しては位置が問題なのではなく、角度が問題なのです＊角度以外に初速も関係します。初速が速いほどコリオリ力は大きくなります。
　閉じる。この話は『並進運動と回転運動』の「回転の中心は任意の位置に設定できる」という話と同じです。

（コリオリ力の解説では円座標が用いられることが多いのですが、ここまでの説明のように直交座標で考えた方が分かりやすいです。）

回転座標系における慣性力

回転座標においては、コリオリ力の他に遠心力もはたらくのですが、こちらは回転中心からの距離によって大きさが変わります。回転中心から離れてるほど遠心力は大きくなります。F = mrω² の r が大きくなれば F も大きくなるということです。

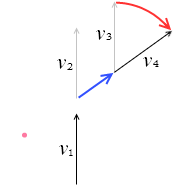v₁ベクトルは v₂ の位置に行きたいところなのですが、遠心力によって v₃ の位置に追いやられ、そしてコリオリ力によって v₄ の向きに曲げられます。左図の青矢印が遠心力で、赤矢印がコリオリ力です。

遠心力は回転座標の中心から外の方向を向いていて、その大きさは中心からの距離に比例し、コリオリ力は速度ベクトルと垂直な方向（座標の回転方向と逆）を向いていて、その大きさは速度の大きさに比例します。

地球表面におけるコリオリ力

ここまでの説明でメリーゴーランド等におけるコリオリ力は理解いただけたと思いますが、地球表面上でのコリオリ力について考えるときはさらに考慮しなければならないことがあります。

それは地球の球面座標を円盤座標に換算しなければならないことです。

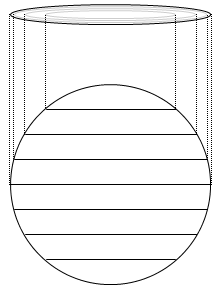たとえば、赤道付近での100kmの移動距離は、北極付近では1km分くらいにしかならなかったりします。

赤道付近での動きは円盤座標に換算されると小さな動きになってしまいます。

地球表面上におけるコリオリ力の大きさは緯度によるのです。

さらに、南半球ではコリオリ力の向きが逆になります。

地上で暮らしていますと、太陽は西へ進んでいきます。これはつまり地球は東へ自転しているということです。北半球の真上、北極上空から地球を見ると左向きに回転しています。逆に南半球の真上、南極上空から地球を見ると右向きに回転しています。

よって、北半球でのコリオリ力は右向きで、南半球でのコリオリ力は左向きになります。