慣性力

慣性力とは

天井から小球がつり下げられていて、床から草が生えてる電車があるとします。

電車が等速で走行しているなら小球は真っ直ぐ垂れていますし、草も真っ直ぐ生えています。

ところが電車が加速すると、小球も草も後ろに傾きます。

ブレーキを掛ければ前に傾きます。

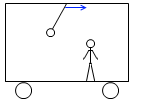これは小球の糸の付け根が右向きに力を受けているのに、小球がその場に踏みとどまろうとするからです。踏みとどまろうとするのは慣性の法則がはたらいているからです。

これは当たり前のことです。当たり前のことですがこれは電車の外にいる観測者＊＝『慣性系⋅非慣性系』項におけるCさんやDさん。
　閉じるから見たときの話です。

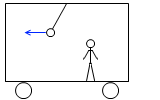電車に乗っている観測者＊＝『慣性系⋅非慣性系』項におけるBさん。
　閉じるから見た場合は、あたかも小球が左向きの力を受けているかのように感じます。

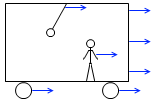観測者も電車も車輪も電車の天井も窓も床も座席も糸の付け根もすべて右向きの力を受けて、すべて同じ加速度で進んでいます。この観測者からは天井も窓も床も座席も静止しているように感じるはずです。

ですので、この観測者からは小球は左向きの力を受けているように感じるわけです。

このように、加速、減速している乗り物に乗った観測者が感じるみかけの力を慣性力といいます＊ 【「みかけ」という言葉の難しさについて】
みかけの力といいますと実在しない力のように聞こえますが、加速中に天井から垂らされた糸の付け根は力を受けます。立っている乗客の足も力を受けます。乗客がよろけそうになるのは足が力を受けるからです。これらは実在する力です。電車のモーター（減速中であればブレーキ）が生み出した力です。その実在する力が糸の付け根や乗客の足に伝わるのです。

しかし、ラジコンヘリコプターがホバリングしている最中に電車が加速した場合についてはどうでしょう。（電車内の観測者から見ると）ラジコンヘリコプターは後方に加速していきます。電車の車体と接触していないものが加速するのです。加速するからには力を受けたはずです（運動の第2法則です）。この場合の力については「みかけ」の力と呼びたくなります。
電車の車体と接触している物には「実在」という言葉を使いたくなり、電車の車体と接触していない物には「みかけ」という言葉を使いたくなります。

電車がとても高性能で、まったく揺れず音もしない場合はどうでしょうか。窓も目隠しされているとします。電車が加速しても減速してもカーブを曲がっても乗客はそのことに気づきません。ただ力を受けます。垂らされた糸は斜めになり、乗客はよろけそうになり、ラジコンヘリコプターは動き出します。このとき「実在」と「みかけ」の差はありますでしょうか。糸や乗客にはたらく力は「実在」で、ラジコンヘリコプターにはたらく力は「みかけ」と区別すべきでしょうか。

こう考えてきますと、「みかけ」は「実在」の反対ではなくもはや同じなのではないかと思えてきます。
　閉じる。慣性の法則によって踏みとどまろうとする力です。観測者が乗った乗り物の加速度と向きが逆の力です。

この慣性力の話は相対速度の話とは違います。加速度が発生していないとだめです。下の話や『慣性系⋅非慣性系』項をよくお読みください。

非慣性系で考える

乗り物に乗った観測者からすると、この慣性力を用いて物理現象を解析する方が楽です。非慣性系で考えるということです。

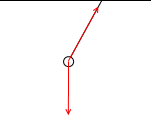電車が右向きに加速しているとき、電車の外にいる観測者、たとえばホームにいる観測者から見ると、小球は右向きに加速しています。

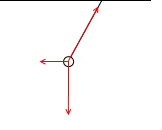
力を図示すると左図のようになります。小球は糸の張力と重力を受けて、そのトータルとして右に加速しています。これがホームにいる観測者からみた運動です。ー慣性系での話です。

電車内にいる観測者には小球は静止して見えます。

電車内にいる観測者にとっての力を図示すると左図のようになります。慣性力と張力と重力がつり合って、小球が静止しています。ー非慣性系での話です。

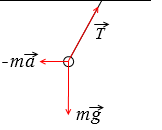電車の加速度を \(\vec{a}\) 、小球の質量を m 、張力を \(\vec{T}\) 、重力加速度を \(\vec{g}\) とすると以下のような式が立てられます。

　　m(- \(\vec{a}\)) + \(\vec{T}\) + m\(\vec{g}\) = 0

鉛直方向の慣性力

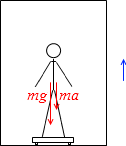慣性力が鉛直方向にはたらくのを感じることができるのがエレベーターです。エレベーター内で体重を測ると、上に加速しているときは体重が重くなり、下に加速しているときは体重が軽くなります＊ 上に加速しているときというのはエレベーターが上昇し始めたときや下降が終わりそうなときです。下に加速しているときというのはエレベーターが下降し始めたときや上昇が終わりそうなときです。『加速度の正負』をよくお読みください。
　閉じる。

人の質量を m [kg] 、エレベーターの加速度を a [m/s²] とすると、

　上に加速中のときの体重は　mg + ma = m(g + a) [N]
　下に加速中のときの体重は　mg - ma = m(g - a) [N]

です。

遊園地のアトラクションのフリーフォールでは、乗り物の加速度が - 9.8 [m/s²] ＊上向きを正としたとき - 9.8 です。
下向きを正とするなら 9.8 です。
m(g - a) = m(9.8 - 9.8) = 0 です。
　閉じるになり、体重が 0 に感じ、無重力状態を楽しめます。エレベーターで例えますとロープが切れた状態です＊日本ではエレベーターのロープが切れる落下事故は起きたことが無いそうです。
　閉じる。

様々な話題の整理

西向きに時速100kmで走るトラックの荷台の上で、ピッチャーが東向きに時速100kmでボールを投げると、ボールは空中で静止します。西にも東にも行きません。その場で静止してから重力でポトンと下に落ちます。ーこれは慣性力の話ではなく、相対速度の話です。

等速走行している電車内でラジコンヘリ（あるいはドローン）を飛び立たせてホバリングさせると、その場で静止します。電車と一緒に走るということです。これはラジコンヘリに初速が与えられているからです。電車と同じスピードの初速が与えられているから静止するのです。ーこれは慣性力の話ではなく、相対速度の話です。

このラジコンヘリがホバリングしている最中に電車が加速すれば、ラジコンヘリは後方に追いやられます。電車が減速すればラジコンヘリは前方へ追いやられます。ーこれは慣性力の話です。

止まっている電車内でラジコンヘリをホバリングさせてから、電車が出発すると、ラジコンヘリは後方へ追いやられます。ーこれは慣性力の話ともいえますが、端的にいえば相対速度の話です。

走行している電車に対して、開いた窓からスタントマンが電車内に飛び込めば、スタントマンは後方へ追いやられます。ーこれは相対速度の話です。

ロープが切れて落下するエレベーター内で衝突直前にジャンプすれば助かるのかという話題がありますが、理屈の上では助かります。実際には、エレベーターの重量が軽すぎるし、人間のジャンプ力が足りなすぎるし、床にも天井にもぶつからないタイミングを図るのが難しいし、実現困難です。ーこれは慣性力の話ともいえますし、相対速度の話ともいえますし、運動量保存の法則も絡んできたりします。

ペットボトルロケット。ー飛ぶ原理を端的に説明する場合は運動量保存の話です。ペットボトルロケットに何らかの観測機器を載せるというなら慣性力の話になります。

カーブを曲がる自動車の中。ーバックミラーに吊るされたキーホルダーがカーブ外側方向へ傾くのは慣性力（遠心力）です。人間がカーブ内側方向に傾くのは慣性力に対抗しようとするためで、人間の意思です。外側に持っていかれないように抵抗しているのです。競輪バンクの傾きも人間の意思によってそうなってます。外側に持っていかれないように、です。

機動戦士ガンダムのスペースコロニー内部。ーあらゆる物体が慣性力（遠心力）によって壁にへばりついてます。