向心力

等速円運動の加速度

等速円運動では、速度の大きさ（つまり速さ）は一定ですが、その向きはたえず変化しています。つまり加速度が生じています。向きを変えるだけでも加速度が必要です。加速度が必要無いのは大きさも向きも変わらないときです。＊様々な運動のうち、加速度が無いものは等速直線運動だけです。
　閉じる

等速円運動の加速度を求めてみます。

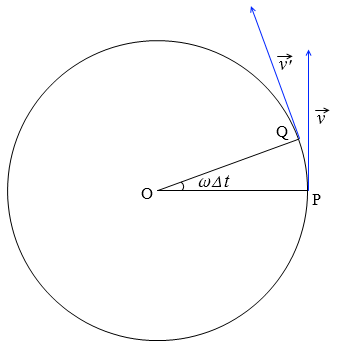半径 r [m] の円周上を速さ v [m/s] で等速円運動している物体が、短い時間 Δt [s] の間にP点からQ点に移動したとします。P点、Q点での速度をそれぞれ \(\vec{v}\) 、\(\vec{v}'\) とします。

このときの角速度を ω [rad/s] とすると 、∠POQ = ωΔt となります。

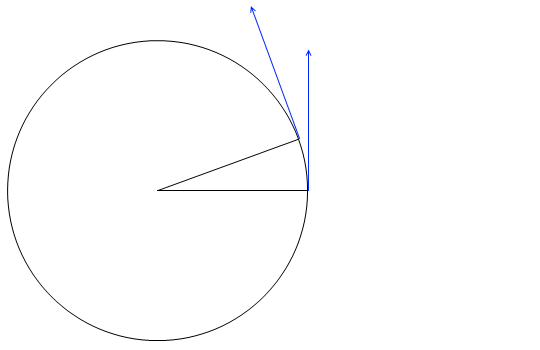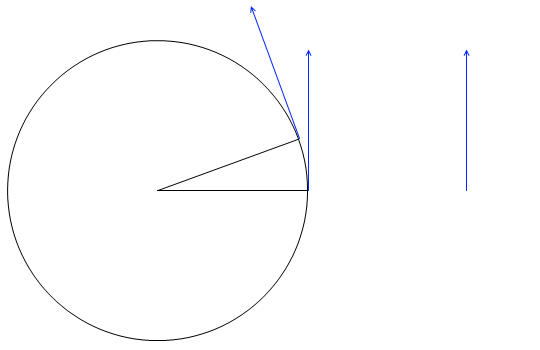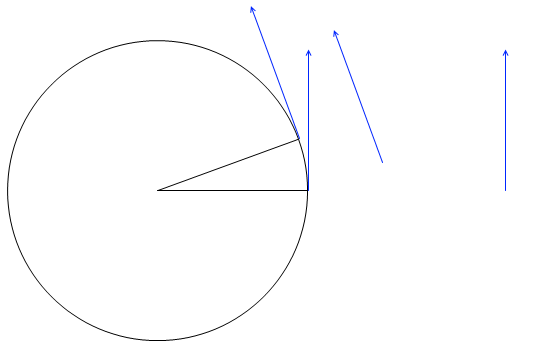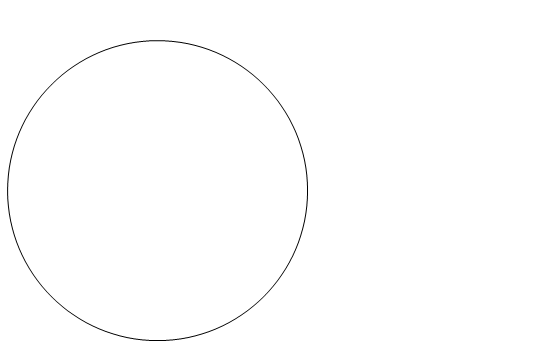
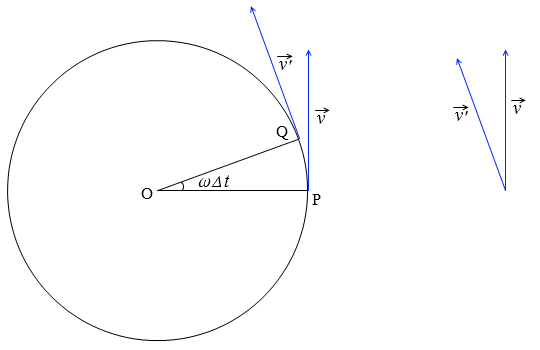すると、\(\vec{v}\) と \(\vec{v}'\) で挟まれた角も ωΔt になります。

（\(\vec{v}\) の方向）=（OP の方向）+（直角）
（\(\vec{v}'\) の方向）=（OP の方向）+（ωΔt）+（直角）
よって
（\(\vec{v}'\) の方向）-（\(\vec{v}\) の方向）=（ωΔt）
となるからです。

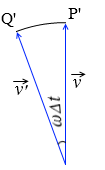ベクトル \(\vec{v}\) の先端をP'、ベクトル \(\vec{v}'\) の先端をQ'とすると、弧P'Q'は vωΔt ＊ 半径 r の円において中心角 1rad の円弧の長さが r なのだから
半径 r の円において中心角 0.8rad の円弧の長さは 0.8r
半径 r の円において中心角 1.2rad の円弧の長さは 1.2r
半径 v の円において中心角 ωΔt [rad] の円弧の長さは vωΔt


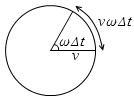
　閉じるとなります。

そしてこのとき ωΔt をどんどん小さくしていくと、弧P'Q'の長さ と 直線P'Q'の長さ は限りなく等しくなっていきます。

つまり ωΔt をどんどん小さくしていくと、vωΔt と | \(\vec{v}'\) - \(\vec{v}\) | は限りなく等しくなっていきます。

ということは Δt が十分小さいとき、 | \(\vec{v}'\) - \(\vec{v}\) | = vωΔt　ということです。

求める加速度ベクトルを \(\vec{a}\) としますと、

　　　　\(\vec{a}\) = \(\large{\frac{\vec{v}'-\vec{v}}{\Delta t}}\)

求める加速度の大きさを a としますと、

　　　　a = \(\large{\frac{|\vec{v}'-\vec{v}|}{\Delta t}}\) = \(\large{\frac{v\omega\Delta t}{\Delta t}}\) = vω

となり、v = rω だからこれを代入して、

　　　　a = rω²

あるいは、ω = \(\large{\frac{v}{r}}\) と変形してから代入して、

　　　　a = \(\large{\frac{v^2}{r}}\)

加速度の向き

　　　　\(\vec{a}\) = \(\large{\frac{\vec{v}'-\vec{v}}{\Delta t}}\)

であることからしますと、\(\vec{a}\) の向きは \(\vec{v}'\) - \(\vec{v}\) の向きです。（分母の Δt に方向はありません。スカラーです。）

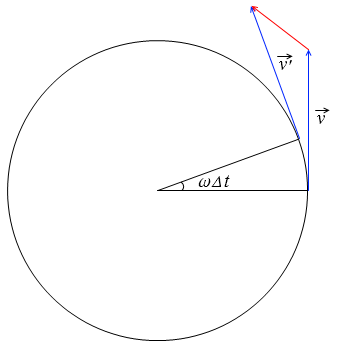この \(\vec{v}'\) - \(\vec{v}\) は左図の赤矢印部分ではありません。ベクトルの起点が合っていません。

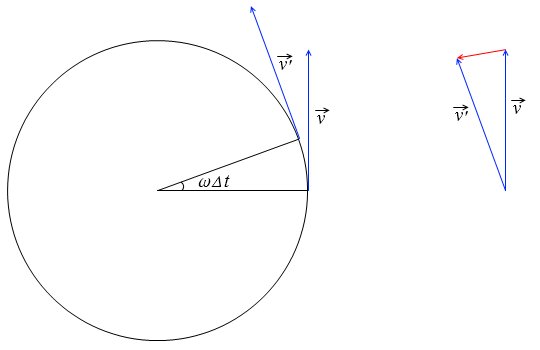かといって左図の赤矢印部分かというと微妙に違います。

上で加速度を求めたときは Δt が十分小さいときの話でした。P点とQ点がごくごく近い場合の加速度（P点での瞬間の加速度）を求めたのです。

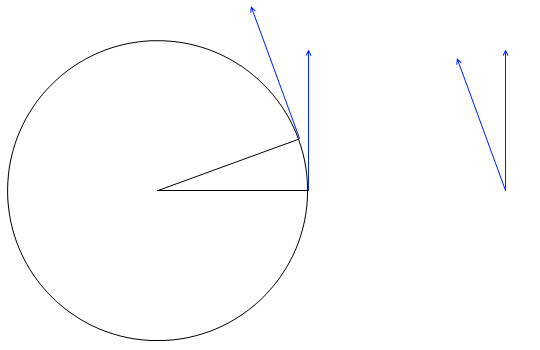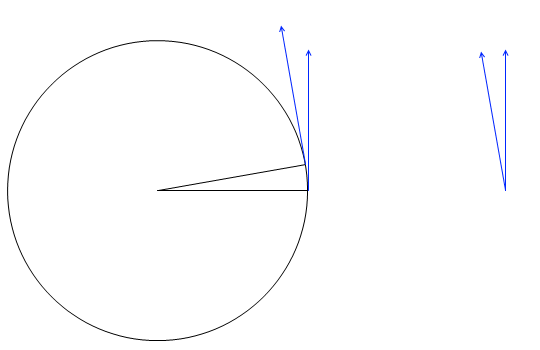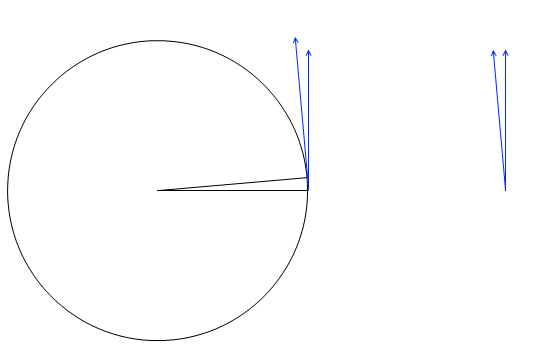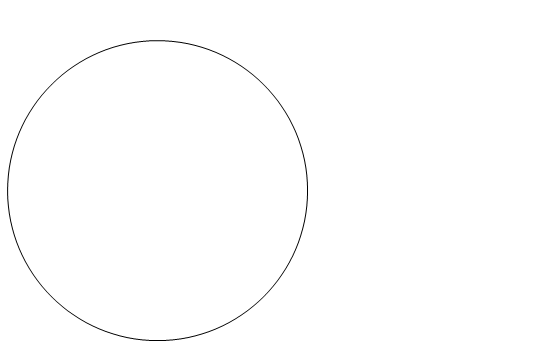ですので図示しますと、\(\vec{v}'\) - \(\vec{v}\) は左図の赤矢印の部分になります。

それを Δt で割ったものが \(\vec{a}\) です。

そして、この矢印は円の中心を向いています。

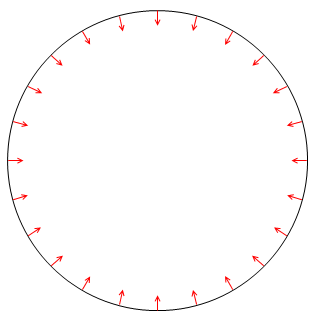これは結構重要なことです。等速円運動では加速度は円の中心を向いているのです。

このように円の中心を向いている加速度を向心加速度といいます。

向心力

等速円運動している物体というのは絶えず上で示した加速度で運動しているわけです。レールに沿って運動しているとしても、ひもで引っ張られて運動しているとしてもです。

等速円運動している物体の質量が m [kg] 、このとき物体にはたらく力が \(\vec{F}\) [N] であるとします。

運動の第2法則　m\(\vec{a}\) = \(\vec{F}\)　によれば、加速度の向きと力の向きは同じなので、等速円運動をしている物体には常に中心向きの力がはたらいているといえます。この力を向心力といいます。

＊
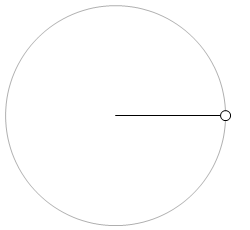
糸の先に付けられた小球が水平面内で等速円運動をしている場合、

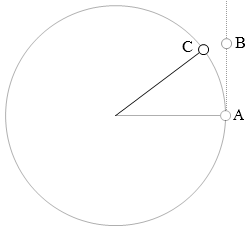
小球は慣性の法則によってB点に行きたいのに、糸による向心力に引っ張られてC点に進みます。このときの向心力の向きを、上で説明したように精密に分析すると、円の中心の方向を向いています。
　閉じる

その大きさは、F = ma　に上で求めた　a = rω² = \(\large{\frac{v^2}{r}}\)　を代入して、

となります。この式は円運動の運動方程式などと呼ばれることがあります。

ちなみに、向心力は物体に仕事をしません。向心力の方向が物体の移動方向と垂直だからです。

また、向心力は物体に初速を与える力とは別物です。混同しないでください。周回の初速を与えたりスピードをUPさせる力は向心力とは別物です。向心力は回転して初めて発生する、中心方向を向いた力です。

『遠心力』項もご参照ください。

まとめ

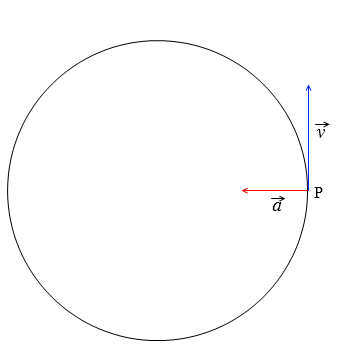等速円運動をする物体がP点を通過する瞬間の速度の方向と加速度の方向を図示すると、左図のようになります。

『円運動』項で求めた速さの式も含めてまとめますと、以下のようになります。

全部を覚えるのが大変でしたら、

　　v = rω
　　a = rω²

の２式だけ覚えておけば、変形することによって他の式を導き出せます。