物体の分裂

静止している物体の分裂

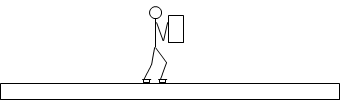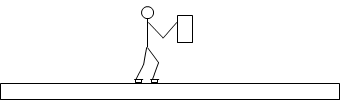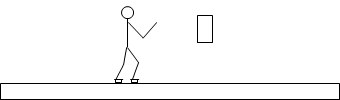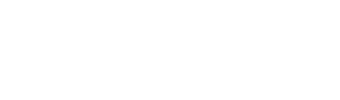スケートリンクの上（摩擦力などの外力がはたらかない条件下）で重い荷物を前方に投げ出すと、投げた人は後ろに後退します。作用⋅反作用の法則です。このときの、人の運動量の変化と荷物の運動量の変化について考えてみます。

人の質量を M [kg] 、荷物の質量を m [kg] 、人が荷物を投げ出す力を \(\vec{F}\) [N] 、力を加えた時間を Δt [s] 、投げた後の人の速度を \(\vec{V}\) [m/s] 、荷物の速度を \(\vec{v}\) [m/s] 、人は始め静止していて、スケートとスケートリンクとの間に摩擦は無いものとします。

『運動量保存の法則』の①式、②式に相当する式を立てますと、

　　人の運動量の変化　：　M\(\vec{V}\) - M⋅0 = - \(\vec{F}\)Δt

　　荷物の運動量の変化　：　m\(\vec{v}\) - m⋅0 = \(\vec{F}\)Δt

\(\vec{F}\)Δt を消去しますと、

　　　　M\(\vec{V}\) = - m\(\vec{v}\)　　……①

この式は、運動量保存の法則の公式に各量を当てはめても求まります。
m₁ → M 、\(\vec{v_1}\) → 0 、m₂ → m 、\(\vec{v_2}\) → 0 、\(\vec{v_1}\)' → \(\vec{V}\) 、\(\vec{v_2}\)' → \(\vec{v}\) としますと、

　　　　M⋅0 + m⋅0 = M\(\vec{V}\) + m\(\vec{v}\)

　∴　　M\(\vec{V}\) = - m\(\vec{v}\)

この式の意味するところは、投げ出した後の人と荷物の運動の向きは反対で、人の質量が大きいほど人の速度は小さくて荷物の速度は大きく、荷物の質量が大きいほど荷物の速度は小さく人の速度は大きいということです。

運動量保存の法則は、内力のみがはたらき、外力がはたらかないときに成り立ちます。今の場合、内力とは、人が荷物を投げる力のことです。外力がはたらく場合というのは、たとえば人がスケート靴でなくスニーカーを履いていたりしてリンクとの間に摩擦があり、荷物を投げても後退しない場合であるとか、あるいは重力の影響をもっと長時間考えて、荷物が床面に落ちるまで考慮したりしますと、外力としての重力がはたらいてしまって運動量保存の法則は成り立たないことになります。今は、スケート靴とスケートリンクの間には摩擦が無いとみなしているのと、運動を考える時間を投げ出し直前と投げ出し直後の短い時間に限定しているので、運動量保存の法則が成り立っているとみなすことができます。

正負についての注意

①式の \(\vec{V}\) と \(\vec{v}\) は向きが逆であるので、①式をスカラーに書き換えるときは、それぞれに V 、- v など＊あるいは - V 、v閉じるという値を代入することになるので、①式は、

　　　　MV = mv

となります。

物体の分裂、結合における正負は、とてもややこしいです。

動いている物体の分裂

次に、すでに動いている物体が分裂する場合を考えてみます。

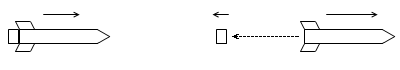速度 \(\vec{V_0}\) [m/s] で進む質量 (M+m) [kg] のロケットが、質量 m [kg] の燃料を相対速度 \(\vec{u}\) [m/s] で噴射したときのロケットの速度 \(\vec{V}\) を求めてみます。

噴射された燃料の実際の速度を \(\vec{v}\) として運動量保存の法則の式を立てますと、

　　　　(M + m) \(\vec{V_0}\) = M \(\vec{V}\) + m \(\vec{v}\)

燃料の速度 \(\vec{v}\) は、相対速度 \(\vec{u}\) と噴射後のロケットの速度 \(\vec{V}\) を用いて　\(\vec{v}\) = \(\vec{V}\) + \(\vec{u}\)　＊相対速度というのは （対象物）-（基準） ですから　\(\vec{u}\) = \(\vec{v}\) - \(\vec{V}\)　です。すなわち　\(\vec{v}\) = \(\vec{V}\) + \(\vec{u}\)　です。
　閉じると表せますので、代入しますと、

　　　　(M + m) \(\vec{V_0}\) = M \(\vec{V}\) + m (\(\vec{V}\)+ \(\vec{u}\))

　∴　　(M + m) \(\vec{V_0}\) = (M + m) \(\vec{V}\) + m \(\vec{u}\)

　∴　　(M + m) \(\vec{V}\) = (M + m) \(\vec{V_0}\) - m \(\vec{u}\)

　∴　　\(\vec{V}\) = \(\vec{V_0}\) - \(\large{\frac{m}{M+m}}\vec{u}\)　　……②

この式より、相対速度 \(\vec{u}\) はロケットの進む向きと逆向きで＊もしロケットの進む向きと同じという場合は、それはロケットを減速させることを意味します。逆噴射ブレーキを掛けるということです。
　閉じる、その大きさが大きいほどロケットは加速しやすく、また噴射燃料の質量 m が大きいほど加速しやすいと分かります。このような理由のため、実際のロケットの体積の大半は燃料タンクとなっていますし、噴射口では燃料を爆発させて相対速度を大きくしています＊実際に地球からロケットを打ち上げる際には空気による摩擦抵抗や重力の影響を大きく受けますので、運動量保存の法則だけを考えることはできません。運動量保存の法則の例えとして考える場合には宇宙空間にいる宇宙船の推進についてイメージする方が適切です。
　閉じる。

ペットボトルロケットというものがありますが、これも同じ原理で加速しています。燃料として水を使い＊水を燃焼させるわけではないので「燃料」という言葉は不適切ですが…。
　閉じる、爆発をさせることはできませんが、高圧でペットボトルの中に閉じ込めて、それを勢い良く吐き出すことによって推力を得ています。

ちなみにですが、気球というものは浮力を利用して飛んでいます。大気よりも気球内部の気体の密度を小さくすることにより浮力を発生させて浮かんでいます。ヘリコプターは空気を掻くことによって飛んでいます。水泳で水を掻いて前に進む原理と同じです。ジェット飛行機はロケットのように燃料を噴射する要素とヘリコプターのように空気を掻く要素の２つを使って飛んでいます。

正負について、前提条件についての注意

上で示した②式　\(\vec{V}\) = \(\vec{V_0}\) - \(\large{\frac{m}{M+m}}\vec{u}\)　を用いて問題を解く場合は、ベクトルをスカラーにして数値を代入するわけですが、相対速度というのはたいてい負の値をとります＊もし正の値をとるというのならそれは逆噴射ブレーキをかけて減速するような場合です。
　閉じるので \(\vec{u}\) の部分には - u というような値が入ることになり、②式は、

　　　　V = V₀ + \(\large{\frac{m}{M+m}}\)u

と書き変わります。＊なお、この式には出てきませんが、燃料の速度 v は負の値をとることも 0 になることも正の値をとることもあります。ロケットの速度と相対速度が向きが逆で大きさが同じとき、燃料の速度は 0 になります。ロケットの速度が大きくて相対速度が小さいときは燃料の速度は正（ロケットと同じ方向）になり、その逆ですと負（ロケットと逆向き）になります。上のロケットのイラストは燃料の速度が負の場合を描いています。
　閉じる

また前提条件として、噴射前のロケットの質量 (M + m) を M 、噴射後の質量 M を (M - m) と設定することも考えられ、そのようなとき②式は、

　　　　\(\vec{V}\) = \(\vec{V_0}\) - \(\large{\frac{m}{M}}\vec{u}\)

と書き変わります。＊ ②式のもとの式
　(M + m) \(\vec{V_0}\) = M \(\vec{V}\) + m \(\vec{v}\)
を
(M + m) → M 、M → (M - m) として書き換えますと、
　M \(\vec{V_0}\) = (M - m) \(\vec{V}\) + m \(\vec{v}\)
　M \(\vec{V_0}\) = (M - m) \(\vec{V}\) + m (\(\vec{V}\) + \(\vec{u}\))
　M \(\vec{V_0}\) = M \(\vec{V}\) + m \(\vec{u}\)
　M \(\vec{V}\) = M \(\vec{V_0}\) - m \(\vec{u}\)
　\(\vec{V}\) = \(\vec{V_0}\) - \(\large{\frac{m}{M}}\vec{u}\)
　閉じる

問題を解くときは問題文をよく読んで間違わないようにしてください。

物体の結合

今度は反対に、物体同士が結合する場合について考えてみます。運動量保存の法則が成り立っている（内力のみがはたらいて外力ははたらかない）ものとします。金属球同士の結合は想像しにくいかもしれませんので、結合器つきの台車や粘土同士の衝突などをイメージしてみてください。（『2物体の反発係数』項の『e = 0』 参照）

質量 m₁ [kg] 、速度 \(\vec{v_1}\) [m/s] の台車Aと、質量 m₂ [kg] 、速度 \(\vec{v_2}\) [m/s] の台車Bが衝突して結合したときの運動量保存の法則の式を立ててみます。

結合後の速度を \(\vec{V}\) [m/s] としますと、

　　　　m₁ \(\vec{v_1}\) + m₂ \(\vec{v_2}\) = (m₁ + m₂) \(\vec{V}\)　　……③

この式も実際に値を代入するときは正負に気を付けなければなりません。

向かい合いの結合

たとえば、AとBが向い合って衝突して結合した場合 \(\vec{v_2}\) には - v₂ という値を代入すべきですから、③式は、

　　　　m₁v₁ - m₂v₂ = (m₁ + m₂) V

となります。このときの V を求めますと、

　　　　V = \(\large{\frac{m_1 v_1 - m_2 v_2}{m_1 + m_2}}\)

右辺の分子に着目しますと、m₁v₁ > m₂v₂ 、つまりAの運動量がBの運動量より大きいとき、V > 0 。つまり結合後もAと同じ方向に進む。m₁v₁ < m₂v₂ ときはその逆、と分かります。よく考えれば当たり前のことです。

片方が止まっているとき

たとえば、Bが止まっているとき、③式は、

　　　　m₁v₁ + m₂⋅0 = (m₁ + m₂) V

　∴　　V = \(\large{\frac{m_1}{m_1 + m_2}}\) v₁

となり、この式を吟味してみますと、m₁ ≫ m₂ のときは V ≒ v₁ 、m₁ ≪ m₂ のときは V ≒ 0 ＊ Aの方が圧倒的に重い場合は、結合後もほぼAの速度を保ち、
Bの方が圧倒的に重い場合は、結合後ほぼ止まってしまうということです。
　閉じるとなることが分かります。

質量が同じとき

たとえば、AとBの質量が同じとき、③式は、

　　　　mv₁ + mv₂ = (m + m) V

　∴　　mv₁ + mv₂ = 2mV

　∴　　v₁ + v₂ = 2V

　∴　　V = \(\large{\frac{v_1+v_2}{2}}\)

となり、結合後の速度はAとBの平均となることが分かります。さらに、v₁ = - v₂ （向い合って等速で衝突して結合）のとき V = 0 となり、v₂ = 0 のときは V の速さは v₁ の半分となることが分かります。