全長 25.0m の一様な太さのニクロム線を図3のように横 10.0m 、たて 5.0m のコの字型に折り曲げ、ニクロム線の両端に電圧 15V の直流電源と電流計を直列に接続した。このとき、ニクロム線に流れる電流は 0.15A であった。
（問3）図4のように、ニクロム線の左端から距離 5.0m の位置に抵抗を接続したところ、電流計の示す電流の値は 0.25A となった。接続した抵抗の大きさはいくらか。
（問4）図4の抵抗をとりはずし、図5のように 20Ω の抵抗をニクロム線と直列に接続した。ニクロム線の左端から距離 L (0≦ L ≦ 10.0m) の位置に銅線を置き、その両端をニクロム線に接続した。電流計の示す電流の値を I とするとき、I と L の関係を表すグラフとして最も適当なものを、下の①～⑤のうちから一つ選べ。ただし、銅線の抵抗は無視できるものとする。
#センター12本試
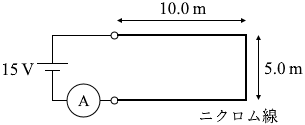
まず、25m のニクロム線の抵抗の大きさを求めますと、オームの法則より、
\(\large{(\frac{V}{I})}\) = \(\large{\frac{15}{0.15}}\) = 100 [Ω]
抵抗は長さに比例するから、1m当たりの抵抗の大きさは
\(\large{\frac{100}{25}}\) = 4.0 [Ω/m]
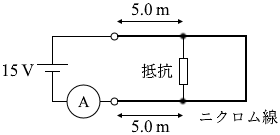
（問3）
ニクロム線の抵抗の大きさが 1m当たり 4.0Ω であるので、図4は以下のような回路であるとみなせます。
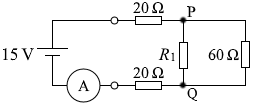
求める抵抗を R1 と置いてPQ間の合成抵抗を求めますと、並列接続ですので、
\(\large{\frac{1}{R_\rm{PQ}}}\) = \(\large{\frac{1}{R_1}}\) + \(\large{\frac{1}{60}}\)
RPQ = \(\large{\frac{60R_1}{R_1+60}}\)
回路全体の合成抵抗を R と置きますと、
R = 20 + RPQ + 20
= 20 + \(\large{\frac{60R_1}{R_1+60}}\) + 20
= 40 + \(\large{\frac{60R_1}{R_1+60}}\) ……➊
15V の電圧を掛けたときに電流計の値が 0.25A となったのだから、オームの法則より、
R = \(\large{\frac{15}{0.25}}\) = 60 ……➋
➊、➋より、
40 + \(\large{\frac{60R_1}{R_1+60}}\) = 60
∴ \(\large{\frac{60R_1}{R_1+60}}\) = 20
∴ 60R1 = 20R1 + 1200
∴ R1 = \(\large{\frac{1200}{40}}\) = 30 [Ω]
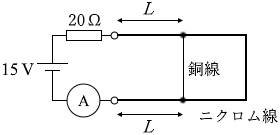
（問4）
銅線には抵抗が無いというのですから電流がいくらでも流れます。ニクロム線側の経路には電流が流れなくなります。図5は実質的に以下のような回路ということになります。
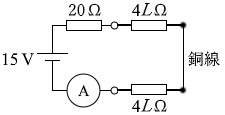
オームの法則（V = RI）より、
15 = (20 + 4L + 4L) × I
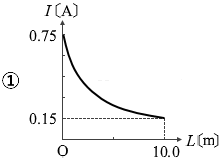
∴ I = \(\large{\frac{15}{20+8L}}\)
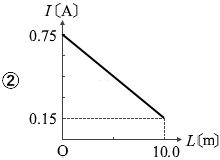
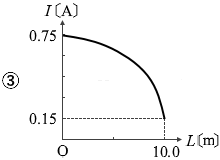
L が 0 のとき I は \(\large{\frac{15}{20}}\) 、L が 10 のとき I は \(\large{\frac{15}{100}}\) であり、この式のグラフの曲線は双曲線（反比例の曲線を左に \(\large{\frac{20}{8}}\) ズラした曲線）になるはずです。
答えは ①