抵抗率
抵抗率とは
『電気抵抗』で、電気抵抗は R = \(\large{\frac{kl}{e^2 nS}}\) であると説明しましたが、この中の各量のうち、形状に関するものとそうでないものを分けて表しますと、
R = \(\large{\frac{kl}{e^2 nS}}\)
= \(\bigl(\large{\frac{k}{e^2 n}}\bigr)\cdot\large{\frac{l}{S}}\)
となります。\(\large{\frac{l}{S}}\) 以外の \(\bigl(\large{\frac{k}{e^2 n}}\bigr)\) の部分は材質の種類による電流の流れにくさを示しています。『電気抵抗』で示した通り、k は流れを妨害する力の係数で、n は自由電子の数密度です。k が大きいほど電流は流れにくく、n が大きいほど電流は大きくなります。このかっこ内の量を 抵抗率(あるいは比抵抗)といい ρ で表します*ρ ロー の逆数は「電気伝導率」という量です。σ シグマ で表します。
ρ という量記号は密度としても用いられます。
閉じる。
抵抗率 ρ
R = ρ⋅\(\large{\frac{l}{S}}\)
抵抗率の単位は、R[Ω] = ρ⋅\(\large{\frac{l[\rm{m}]}{S[\rm{m}^2]}}\) ⇒ ρ = \(\large{\frac{R[Ω]S[\rm{m}^2]}{l[\rm{m}]}}\) ですので、[Ω⋅m] オームメートル です。
銅の抵抗率は 0 ℃で ρ銅 = 1.55×10-8 Ω⋅m 、
鉄の抵抗率は 0 ℃で ρ鉄 = 8.9×10-8 Ω⋅m で、
鉄の方が材質的には 6倍くらい電気を通しにくいのですが、抵抗器を作るときは、断面積 S を 6倍にするか、もしくは長さを \(\large{\frac{1}{6}}\) 倍にすれば、銅で作ったときと同じくらいの抵抗にすることができます。
このように抵抗を抵抗率を使って表現すると、抵抗の特徴をはっきり認識することができます。
 R = ρ⋅\(\large{\frac{l}{S}}\) において ρ が一定のとき、
R = ρ⋅\(\large{\frac{l}{S}}\) において ρ が一定のとき、
 l を 2倍にすると R は 2倍になるわけですが、
l を 2倍にすると R は 2倍になるわけですが、
 これは2つの抵抗器を直列につないだのと同等とみなすことができます。
これは2つの抵抗器を直列につないだのと同等とみなすことができます。
 S を 2倍にすると R は \(\large{\frac{1}{2}}\) 倍になるわけですが、
S を 2倍にすると R は \(\large{\frac{1}{2}}\) 倍になるわけですが、
 これは2つの抵抗器を並列につないだのと同等とみなすことができます。
これは2つの抵抗器を並列につないだのと同等とみなすことができます。
 抵抗率 ρ が一定のとき(材質が同一のとき)、太くて短い方が電流は流れやすく、細くて長い方が電流は流れにくいです。
抵抗率 ρ が一定のとき(材質が同一のとき)、太くて短い方が電流は流れやすく、細くて長い方が電流は流れにくいです。
抵抗率の温度変化
抵抗率は温度によって変化します。温度が高くなると抵抗率が大きくなります。自由電子は陽イオンにぶつかりながら進んでいきますが、温度が高くなると陽イオンの振動が激しくなり、自由電子の進行を邪魔するのです。*半導体という物質では逆に温度が上がるほど抵抗率が小さくなったりします。
閉じる
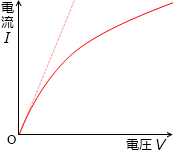 電圧を上げていくと、ジュール熱で温度が上がり、抵抗率が大きくなっていき、電流と電圧の関係が直線ではなくなります。
電圧を上げていくと、ジュール熱で温度が上がり、抵抗率が大きくなっていき、電流と電圧の関係が直線ではなくなります。
温度が 1℃ 上がるごとの抵抗率の変化量を抵抗率の温度係数といい、α アルファ で表します。0 ℃ のときの抵抗率を ρ0 [Ω⋅m] 、t [℃] のときの抵抗率を ρ [Ω⋅m] とすると、ほとんどの物質において以下の関係が成り立っています。
抵抗率の温度係数 α
ρ = ρ0 (1 + αt)
α の単位は [/℃] です*あるいは [/K] としている参考書もあります。
ρ = ρ0 (1 + αt) という式についても、
ρ = ρ0 {1 + α(T-T0)} としている場合があります。この場合は温度の単位が ℃ であるとも K ケルビン であるとも解釈出来ます。
℃ と K は基準が違うだけで目盛り幅は一緒なのでたいした違いはありません。でも混同しやすいので問題が出題されたときは注意が必要です。
さらに厳密なことをいうと本当の関係式は、
ρ = ρ0 (1 + α t + β t2 + γ t3) だったりします。
閉じる。ケルビン温度でなくセルシウス温度です。
抵抗率と温度係数の数値の例をいくつか挙げておきます。( 0℃~100℃ の場合の平均温度係数を調べてみました。20℃の場合や 0℃~300℃ の場合は数値が違ってきます。)
| 物質の種類 | 0℃での抵抗率 ρ0 [×10-8 Ω⋅m] | 抵抗率の温度係数 α [×10-3 /℃] |
|---|---|---|
| 銅 | 1.55 | 4.4 |
| 鉄 | 8.9 | 6.5 |
| タングステン | 4.9 | 4.9 |
| ニクロム | 107 | 0.21 |
タングステンというのは白熱電球のフィラメントに使われる素材です。
ニクロムというのは電熱器によく使われる合金です。ニクロムの温度係数の値は資料によってまちまちで正確な数値は分かりませんでした。でもかなり小さいことは確かです。抵抗率の温度係数が小さいということは温度変化に強いということです。ニクロムは抵抗率が大きく(抵抗が大きいので太くすることができ、壊れにくい*抵抗率が小さい物質で太いものを作ると電流が流れすぎるので危険です。だから細くしなければならないけれども、そうすると今度は丈夫な製品が作れない。抵抗率の程度がちょうどいいのがニクロムということです。
でも今はもっと具合のいい物質が発見されてニクロムは使われなくなっているそうです。
閉じる)、温度変化にも強いので電熱器によく使われます。「ニクロム線」という言葉を聞いたことはありませんでしょうか?
話を整理
『電気抵抗』のところからの話の流れを数式で整理してみます。
I = \(\bigl(\large{\frac{e^2 nS}{kl}}\bigr)\)V
\(\bigl(\large{\frac{e^2 nS}{kl}}\bigr)\) = \(\large{\frac{1}{R}}\)
R = \(\large{\frac{kl}{e^2 nS}}\)
= \(\bigl(\large{\frac{k}{e^2 n}}\bigr)\cdot\large{\frac{l}{S}}\)
\(\bigl(\large{\frac{k}{e^2 n}}\bigr)\) = ρ
ρ = ρ0 (1 + αt)
また、
R = ρ⋅\(\large{\frac{l}{S}}\) R0 = ρ0⋅\(\large{\frac{l}{S}}\) ρ = ρ0 (1 + αt)
であることから、1番目、2番目の式を変形して、
ρ = R⋅\(\large{\frac{S}{l}}\) ρ0 = R0⋅\(\large{\frac{S}{l}}\)
これらを3番目の式に代入しますと、
R⋅\(\large{\frac{S}{l}}\) = R0⋅\(\large{\frac{S}{l}}\) (1 + αt)
∴ R = R0 (1 + αt)
となりますので、
ρ = ρ0 (1 + αt) であるならば R = R0 (1 + αt) であるということがいえます。