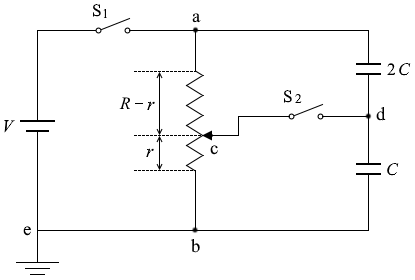
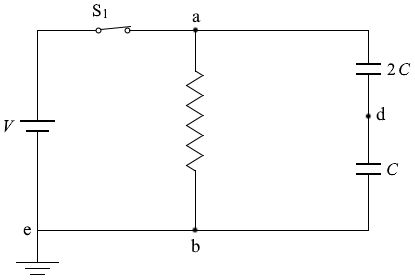
(問4)1 のみ閉じたということなので実質的な回路は、
V 、二つのコンデンサーに V の電圧が掛かります。
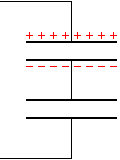
V d と置くと、上のコンデンサーに掛かる電圧は V - V d です。
Q 1 とすると、下のコンデンサーにも Q 1 の電気量が蓄えられています 。*
直列につながれたコンデンサー においては閉じる
よって、Q = CV
上のコンデンサー: Q 1 = 2C × (V - V d )
下のコンデンサー: Q 1 = C × V d
であるので、
2C (V - V d ) = CV d
∴ 2V - 2V d = V d
∴ 2V = 3V d
∴ V d = \(\large{\frac{2}{3}}\)V
と求まります。
下のコンデンサーに掛かる電圧が \(\large{\frac{2}{3}}\)V なので、上のコンデンサーに掛かる電圧は V - \(\large{\frac{2}{3}}\)V = \(\large{\frac{1}{3}}\)V です。直列の二つのコンデンサーに掛かるそれぞれの電圧は、電気容量の逆比ということです。
(別解)
合成容量 を C 1 としますと、
\(\large{\frac{1}{C_1}}\) = \(\large{\frac{1}{2C}}\) + \(\large{\frac{1}{C}}\)
∴ \(\large{\frac{1}{C_1}}\) = \(\large{\frac{1+2}{2C}}\)
∴ \(\large{\frac{1}{C_1}}\) = \(\large{\frac{3}{2C}}\)
∴ C 1 = \(\large{\frac{2}{3}}\)C
ここに V の電圧が掛かるのだから、合成容量に蓄えられた電気量を Q 1 とすると、Q = CV
Q 1 = \(\large{\frac{2}{3}}\)C × V
この電気量は、下のコンデンサーの電気量でもあるので、Q = CV の関係より、
V d = \(\large{\frac{Q_1}{C}}\) = \(\large{\frac{\frac{2}{3}CV}{C}}\) = \(\large{\frac{2}{3}}\)V
と求まります。
(まず、V d を求めます)1 とスイッチS2 を閉じた場合、左図の V r V d が同じで、V R -r V - V d が同じです。
I 1 としますと、オームの法則 より、
I 1 = \(\large{\frac{V}{R}}\)
です。
よって、
V r rI 1 = r \(\large{\frac{V}{R}}\) = \(\large{\frac{r}{R}}\)V
であり、これが V d です。
(慣れてる人は暗算で導き出せると思います。直列接続では、電圧の比は抵抗の比です。)
(次に、静電エネルギーを求めます)静電エネルギー :\(\large{\frac{1}{2}}\)⋅2C ⋅(V - V d )2 = C ⋅(V - \(\large{\frac{r}{R}}\)V )2 = C (\(\large{\frac{R-r}{R}}\)V )2
下のコンデンサーの静電エネルギー:\(\large{\frac{1}{2}}\)CV d 2 = \(\large{\frac{1}{2}}\)C (\(\large{\frac{r}{R}}\)V )2
総和 U は
U = C (\(\large{\frac{R-r}{R}}\)V )2 + \(\large{\frac{1}{2}}\)C (\(\large{\frac{r}{R}}\)V )2
です。
r = 0 のとき、
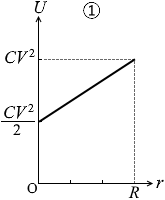
U = C (\(\large{\frac{R-0}{R}}\)V )2 + \(\large{\frac{1}{2}}\)C (\(\large{\frac{0}{R}}\)V )2 = CV 2
r = R のとき、
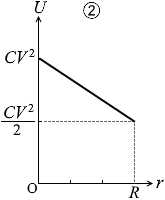
U = C (\(\large{\frac{R-R}{R}}\)V )2 + \(\large{\frac{1}{2}}\)C (\(\large{\frac{R}{R}}\)V )2 = \(\large{\frac{1}{2}}\)CV 2
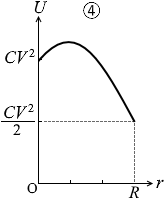
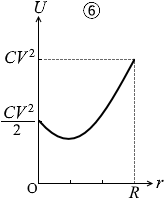
このようになっているグラフは②か④か⑤です。
そして、r の2次関数の式になっていますので、グラフの曲線は放物線のはずです。
さらに、平方完成の形に変形しますと、
U = C (\(\large{\frac{R-r}{R}}\)V )2 + \(\large{\frac{1}{2}}\)C (\(\large{\frac{r}{R}}\)V )2
= C \(\Big\{\)(\(\large{\frac{R}{R}}\)V )2 - 2\(\large{\frac{r}{R}}\)V 2 + (\(\large{\frac{r}{R}}\)V )2 \(\Big\}\) + \(\large{\frac{1}{2}}\)C (\(\large{\frac{r}{R}}\)V )2
= CV 2 - 2C \(\large{\frac{r}{R}}\)V 2 + C (\(\large{\frac{r}{R}}\)V )2 + \(\large{\frac{1}{2}}\)C (\(\large{\frac{r}{R}}\)V )2
= CV 2 - 2C \(\large{\frac{r}{R}}\)V 2 + \(\large{\frac{3}{2}}\)C (\(\large{\frac{r}{R}}\)V )2
= \(\large{\frac{3}{2}}\)C (\(\large{\frac{r}{R}}\)V )2 - 2C \(\large{\frac{r}{R}}\)V 2 + CV 2
= \(\large{\frac{3CV^2}{2R^2}}\)r 2 - 2C \(\large{\frac{V^2}{R}}\)r + CV 2
= \(\large{\frac{3CV^2}{2R^2}}\)\(\Big\{\)r 2 - 2r \(\Big\}\) + CV 2
= \(\large{\frac{3CV^2}{2R^2}}\)\(\Big\{\)r 2 - 2r + (\(\large{\frac{2R}{3}}\))2 - (\(\large{\frac{2R}{3}}\))2 \(\Big\}\) + CV 2
= \(\large{\frac{3CV^2}{2R^2}}\)\(\Big\{\)r 2 - 2r + (\(\large{\frac{2R}{3}}\))2 \(\Big\}\) - \(\large{\frac{2}{3}}\)CV 2 + CV 2
= \(\large{\frac{3CV^2}{2R^2}}\)\(\Big\{\)r - 2 + \(\large{\frac{1}{3}}\)CV 2
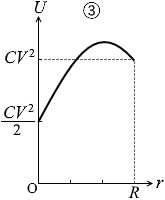
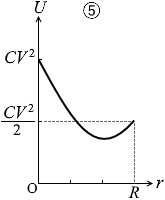
となり、\(\large{\frac{3CV^2}{2R^2}}\) > 0 なので、グラフの曲線は下に凸であり、また、r = \(\large{\frac{2R}{3}}\) のときに最小値 U = \(\large{\frac{1}{3}}\)CV 2 をとると分かります。
このようなグラフは ⑤ です。
(別に平方完成の形にしなくても r 2 の係数の正負を確かめれば上に凸の曲線か下に凸の曲線かが分かるので、選択肢の中のどれであるかは特定できます。)
(余談)r = 0 のときというのは V r V d = 0 であり、静電エネルギーの総和というのは上のコンデンサーに蓄えられた静電エネルギーのことです。下のコンデンサーには電圧が掛からず電荷も溜まりません。総和としては最大です。
逆に、r = R のときというのは、上のコンデンサーには電荷が溜まらず、静電エネルギーの総和というのは下のコンデンサーに蓄えられた静電エネルギーのことです。
総和が最小となる r = \(\large{\frac{2R}{3}}\) のときというのは、V d = \(\large{\frac{2 }{3}}\)V であり、上の問4の場合のことであり、スイッチS2 を開いているのと同じ状態ということです。二つのコンデンサーが充電される過程でdc間に電流が流れないということです。
 このようになり、
このようになり、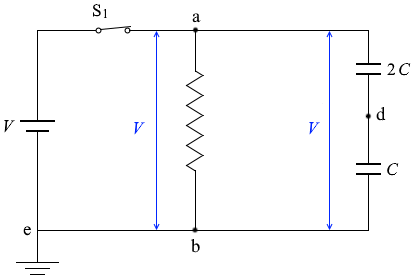 抵抗に V 、二つのコンデンサーに V の電圧が掛かります。
抵抗に V 、二つのコンデンサーに V の電圧が掛かります。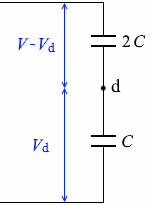 求める点dの電位を Vd と置くと、上のコンデンサーに掛かる電圧は V - Vd です。
求める点dの電位を Vd と置くと、上のコンデンサーに掛かる電圧は V - Vd です。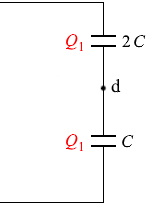 また、上のコンデンサーに蓄えられた電気量を Q1 とすると、下のコンデンサーにも Q1 の電気量が
また、上のコンデンサーに蓄えられた電気量を Q1 とすると、下のコンデンサーにも Q1 の電気量が
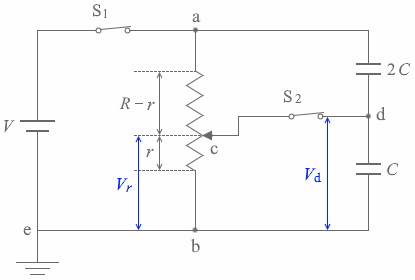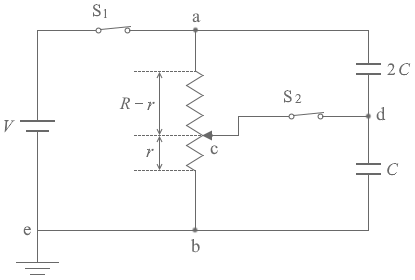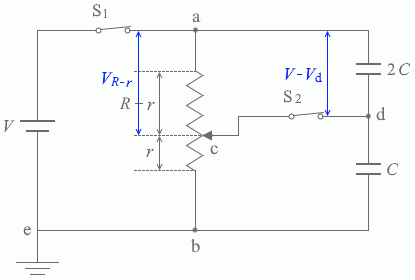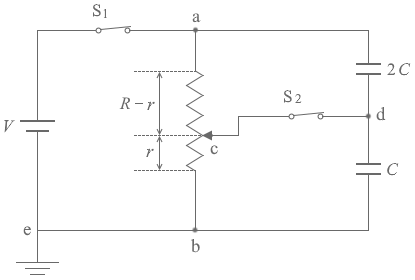 スイッチS1とスイッチS2を閉じた場合、左図の Vr と Vd が同じで、VR-r と V - Vd が同じです。
スイッチS1とスイッチS2を閉じた場合、左図の Vr と Vd が同じで、VR-r と V - Vd が同じです。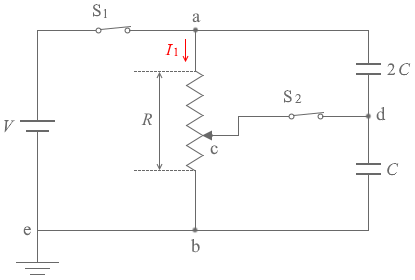 そして、ab間を流れる電流を I1 としますと、
そして、ab間を流れる電流を I1 としますと、