qG93B

（問1）
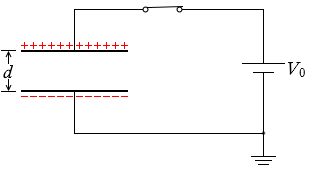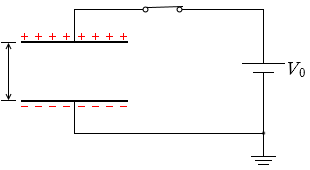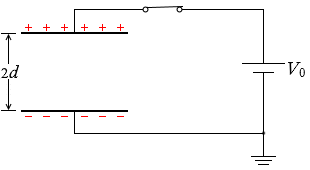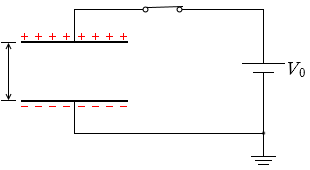
C = \(\large{\frac{1}{4\pi k}\frac{S}{d}}\) の関係より、電気容量 C は極板間 d に反比例しますので、極板間が2倍になると電気容量は \(\large{\frac{1}{2}}\) になり、

Q = CV の関係より、電圧 V が一定で電気容量 C が \(\large{\frac{1}{2}}\) になると、電荷（電気量）Q は \(\large{\frac{1}{2}}\)倍 になります。（抱えきれない電荷が電池に戻っていくようなイメージです）

つまり、コンデンサーに蓄えられた電荷は Q₀ の \(\large{\frac{1}{2}}\)倍 になります。

（問2）
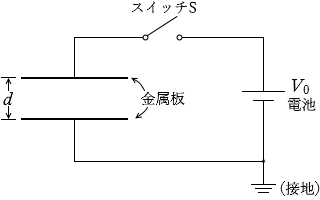
上のアニメーションで示したように、スイッチSを閉じたまま極板間を d に戻すと電荷（電気量）は元の Q₀ に戻ります。

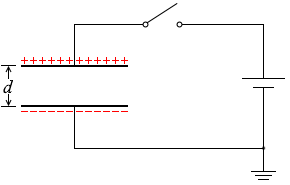そして、スイッチSを開いてから

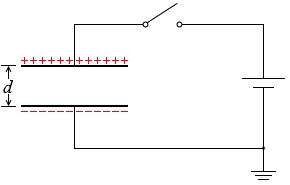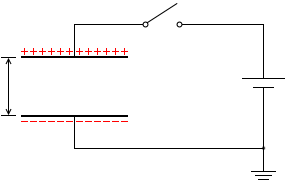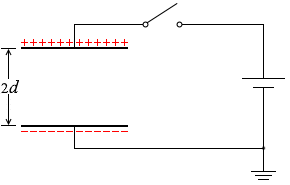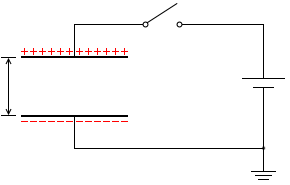極板間の距離を広げても電気量は変化しません。電荷は逃げようがありません。

極板間が2倍になったので電気容量は \(\large{\frac{1}{2}}\) になり、

静電エネルギーには U = \(\large{\frac{Q^2}{2C}}\) という関係があり（U はここでは W のこと）、Q の2乗に比例し C に反比例しますので、Q が一定で C が \(\large{\frac{1}{2}}\) になると、U は2倍になります。

つまり、静電エネルギーは W₀ の 2倍 になります。

（別解:1）
Q = CV の関係より、電気量 Q が一定で電気容量 C が \(\large{\frac{1}{2}}\) になると、電圧 V は2倍になります。（電位差 V と電場 E と距離 d には V = Ed という関係があります）

静電エネルギーには U = \(\large{\frac{1}{2}}\)QV という関係があるので、Q が一定で V が2倍になると、U は2倍になります。

（別解:2）
極板間が d のときの静電エネルギー W₀ は

　　　（ U = \(\large{\frac{1}{2}}\)QV の関係より ）

　　　　W₀ = \(\large{\frac{1}{2}}\)Q₀V₀

ですが、

このときの極板間引力（F₀ と置く。また極板間の電場の強さを E₀ と置く）は

　　　（ F = \(\large{\frac{1}{2}}\)QE の関係より ）

　　　　F₀ = \(\large{\frac{1}{2}}\)Q₀E₀

d から 2d に広がるまで電荷が変わらないのだから極板間の電場の強さ（E₀ と置く）も変わりません。Q₀ も E₀ も変わらないわけです。ということは（上式より）F₀ も変わらないということです。コンデンサーが電池に接続されているときは極板間を広げると極板間引力は変わりますが、電池に接続されていないときは極板間引力は変わらないのです。

そして、d から 2d に広げたことによって増える静電エネルギーというのは、d から 2d に広げるまでにした仕事の大きさです（『一様な電場での位置エネルギー』、『静電エネルギーの差は仕事の大きさであることから求める』参照）。

この増加分の静電エネルギーを W₂' と置きますと、

　　　　W₂' = F₀ × d = \(\large{\frac{1}{2}}\)Q₀E₀ × d

（V = Ed という関係があるので）V₀ = E₀d であり、これを代入すると、

　　　　W₂' = \(\large{\frac{1}{2}}\)Q₀V₀

これは W₀ と同じ大きさであり、つまり静電エネルギーは2倍になります。

（余談）
問1の静電エネルギーを W₁ 、問2の静電エネルギーを W₂ として3種の静電エネルギーをまとめますと、

　　　　W₀ = \(\large{\frac{1}{2}}\)Q₀V₀　　＊ 閉じる

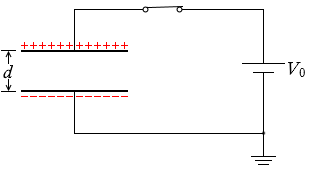
　　　　W₁ = \(\large{\frac{1}{4}}\)Q₀V₀　　＊ 電圧は変わらず電荷が半分になるから
　　W₁ = \(\large{\frac{1}{2}}\)(\(\large{\frac{1}{2}}\)Q₀)V₀ = \(\large{\frac{1}{4}}\)Q₀V₀

閉じる

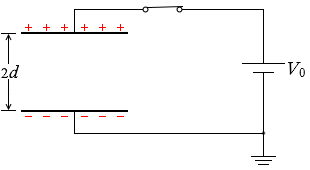
　　　　W₂ = Q₀V₀　　＊ 　　W₂ = W₀ + W₂' = \(\large{\frac{1}{2}}\)Q₀V₀ + \(\large{\frac{1}{2}}\)Q₀V₀ = Q₀V₀
と考えてもいいし、
電荷は変わらず電圧が2倍になるから
　　W₂ = \(\large{\frac{1}{2}}\)Q₀(2V₀) = Q₀V₀
と考えてもいい。


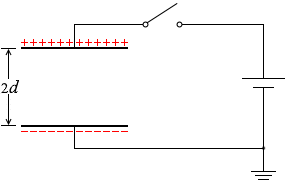
電荷が変わらないので電場も変わらない。
そして極板間距離が2倍になるということは
（V = Ed という関係があるので）電圧は2倍になるということ。
つまりこのときの電圧は 2V₀ 閉じる

（問3）
「再び極板間の距離を d に戻し」ても、上のアニメーションで示したように電気量は変わらず、「スイッチSを閉じて十分に時間が経った」ということは、これはこの問題の一番始めの状態に戻したということであり、「スイッチSを開いた」としても電気量は変わりません。Q₀ ということです。

そして、「比誘電率 2 の誘電体をすきまなく入れると」、電気容量は2倍になり、

Q = CV の関係がありますので、Q が一定で C が2倍になれば、V は \(\large{\frac{1}{2}}\) になります。

つまり、極板間の電位差は V₀ の \(\large{\frac{1}{2}}\)倍 になります。