(問1)
(まず真空中での電気容量 C の式を立てる)d 、長方形の極板の 2a ではない方の辺の長さを b 、真空の誘電率を ε 0 とします。そうしますと、真空中のコンデンサーの電気容量 (C = ε \(\large{\frac{S}{d}}\))の式は
C = ε 0 \(\large{\frac{2ab}{d}}\) ……①
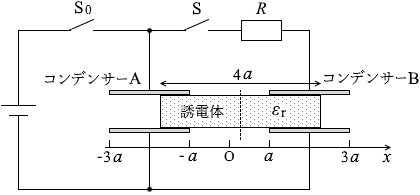
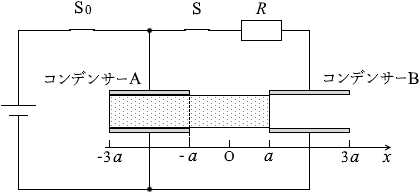
(C A 、C B の式を立てる)コンデンサーは横方向に分割できる とみなせるので、
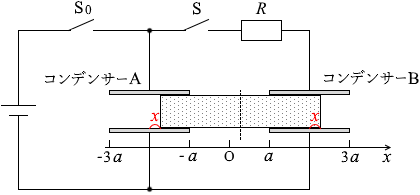
コンデンサーAは、a +x の真空中のコンデンサーと、a -x の誘電体を挟んだコンデンサーが並列に接続されているとみなし、
C A = ε 0 \(\large{\frac{(a+x)b}{d}}\) + ε r ε 0 \(\large{\frac{(a-x)b}{d}}\)
= ε 0 \(\large{\frac{(a+x)+ε_r(a-x)}{d}}\)b ……②
同様に、コンデンサーBは、a +x の誘電体を挟んだコンデンサーと、a -x の真空中のコンデンサーが並列に接続されているとみなし、
C B = ε r ε 0 \(\large{\frac{(a+x)b}{d}}\) + ε 0 \(\large{\frac{(a-x)b}{d}}\)
= ε 0 \(\large{\frac{ε_r(a+x)+(a-x)}{d}}\)b ……③
(自分で設定した d 、b 、ε 0 を消去)
ε 0 \(\large{\frac{2ab}{d}}\) = C
ε 0 \(\large{\frac{b}{d}}\) = \(\large{\frac{C}{2a}}\)
これを②式に代入して、
C A = \(\large{\frac{(a+x)+ε_r(a-x)}{2a}}\)C
= \(\large{\frac{a+x+ε_ra-ε_rx}{2a}}\)C
= \(\large{\frac{-(ε_r-1)x+(ε_r+1)a}{2a}}\)C
同様に、③式に代入して、
C B = \(\large{\frac{ε_r(a+x)+(a-x)}{2a}}\)C
= \(\large{\frac{ε_ra+ε_rx+a-x}{2a}}\)C
= \(\large{\frac{(ε_r-1)x+(ε_r+1)a}{2a}}\)C
コンデンサーは誘電体を挟むと電気容量が大きくなる ものですが、上の2式を見ますと、x が大きくなるほど(誘電体が右にズレていくほど)、C A の値は小さくなり、C B の値は大きくなるようにちゃんとなっています。
(問2)
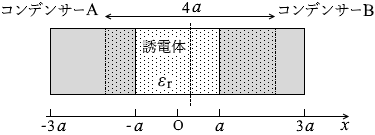
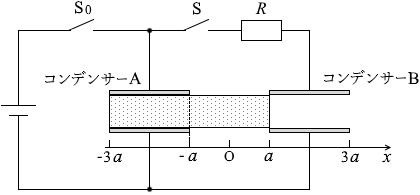
このとき、C A = ε r C 、C B = C であり 、電源の電圧を V としますと各電気量 は、
Q A = C A V = ε r C V ……④
Q B = C B V = C V ……⑤
題意より Q = Q A + Q B だから、
Q = ε r C V + C V
∴ \(\large{\frac{Q}{ε_rC+C}}\) = V
これを④式、⑤式に入れ戻しますと、
Q A = ε r C \(\large{\frac{Q}{ε_rC+C}}\) = \(\large{\frac{ε_r}{ε_r+1}}\)Q
Q B = C \(\large{\frac{Q}{ε_rC+C}}\) = \(\large{\frac{1}{ε_r+1}}\)Q
(問3)
誘電体を動かす前にスイッチは開かれているので、コンデンサーA、Bに蓄えられた電気量 Q A 、Q B の値は問2のままです。
電気容量は x によって変化しますが、その値は問1で求めました。
すなわち、
C A = \(\large{\frac{-(ε_r-1)x+(ε_r+1)a}{2a}}\)C
C B = \(\large{\frac{(ε_r-1)x+(ε_r+1)a}{2a}}\)C
Q A = \(\large{\frac{ε_r}{ε_r+1}}\)Q
Q B = \(\large{\frac{1}{ε_r+1}}\)Q
この各値をコンデンサーの静電エネルギー の式( U = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{Q^2}{C}}\) )に代入しますと、
U A = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{A}}^2}{C_\rm{A}}}\)
= \(\large{\frac{1}{2}}\)⋅\(\Large{\frac{(\frac{ε_r}{ε_r+1}Q)^2}{\frac{-(ε_r-1)x+(ε_r+1)a}{2a}C}}\)
= \(\large{\frac{(\frac{ε_r}{ε_r+1}Q)^2a}{\{-(ε_r-1)x+(ε_r+1)a\}C}}\)
= \(\large{\frac{{ε_r}^2Q^2a}{(ε_r+1)^2\{-(ε_r-1)x+(ε_r+1)a\}C}}\)
U B = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{B}}^2}{C_\rm{B}}}\)
= \(\large{\frac{1}{2}}\)⋅\(\Large{\frac{(\frac{1}{ε_r+1}Q)^2}{\frac{(ε_r-1)x+(ε_r+1)a}{2a}C}}\)
= \(\large{\frac{(\frac{1}{ε_r+1}Q)^2a}{\{(ε_r-1)x+(ε_r+1)a\}C}}\)
= \(\large{\frac{Q^2a}{(ε_r+1)^2\{(ε_r-1)x+(ε_r+1)a\}C}}\)
(問4)
スイッチSが閉じられる直前までは、引き続き、コンデンサーA、Bに蓄えられた電気量 Q A 、Q B の値は問2のままであり、
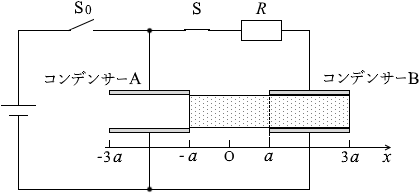
各電気容量は、x = a であるので、
C A = C
C B = ε r C
であり、このときのコンデンサーAの電圧を V A 、コンデンサーBの電圧を V B とすると、(Q = CV
V A = \(\large{\frac{Q_\rm{A}}{C_\rm{A}}}\) = \(\large{\frac{ε_r}{ε_r+1}}\)Q ⋅\(\large{\frac{1}{C}}\) = \(\large{\frac{ε_r}{ε_r+1}}\)⋅\(\large{\frac{Q}{C}}\)
V B = \(\large{\frac{Q_\rm{B}}{C_\rm{B}}}\) = \(\large{\frac{1}{ε_r+1}}\)Q ⋅\(\large{\frac{1}{ε_rC}}\) = \(\large{\frac{1}{(ε_r+1)ε_r}}\)⋅\(\large{\frac{Q}{C}}\)
ε r > 1 であるので V A > V B であり、抵抗に流れる電流は 右向き とわかります。
I 0 )を求めるためにキルヒホッフの第2法則 の式を立てますと、
\(\large{\frac{ε_r}{ε_r+1}}\)⋅\(\large{\frac{Q}{C}}\) - RI 0 - \(\large{\frac{1}{(ε_r+1)ε_r}}\)⋅\(\large{\frac{Q}{C}}\) = 0
∴ RI 0 = \(\large{\frac{ε_r}{ε_r+1}}\)⋅\(\large{\frac{Q}{C}}\) - \(\large{\frac{1}{(ε_r+1)ε_r}}\)⋅\(\large{\frac{Q}{C}}\)
∴ I 0 = \(\big\{\large{\frac{ε_r}{ε_r+1}}\) - \(\large{\frac{1}{(ε_r+1)ε_r}}\}\)⋅\(\large{\frac{Q}{CR}}\)
= \(\big\{\large{\frac{{ε_r}^2-1}{(ε_r+1)ε_r}}\}\)⋅\(\large{\frac{Q}{CR}}\)
= \(\big\{\large{\frac{(ε_r+1)(ε_r-1)}{(ε_r+1)ε_r}}\}\)⋅\(\large{\frac{Q}{CR}}\)
= \(\large{\frac{(ε_r-1)Q}{ε_rCR}}\)
(問5)
抵抗で発生するジュール熱というのは、2つのコンデンサーの静電エネルギーの減少量と同等です。エネルギーは他に逃れる先が無いので、静電エネルギーの減少分は全てジュール熱に使われます。
スイッチSを閉じる前の静電エネルギーは問3で求めましたが、スイッチSを閉じた後の静電エネルギーを改めて求めてみます。
スイッチSを閉じて十分に時間が経過した後の、コンデンサーA、Bに蓄えられた電気量を Q A ' 、Q B ' 、コンデンサーA、Bに蓄えられた静電エネルギーを U A ' 、U B ' とします。
各コンデンサーの電気容量は問4と同じく、
C A = C
C B = ε r C
であり、スイッチSを閉じて十分に時間が経過した後は2つのコンデンサーの電圧 ( V = \(\large{\frac{Q}{C}}\) )は等しくなっていますから、
\(\large{\frac{Q_\rm{A}'}{C_\rm{A}}}\) = \(\large{\frac{Q_\rm{B}'}{C_\rm{B}}}\)
∴ \(\large{\frac{Q_\rm{A}'}{C}}\) = \(\large{\frac{Q_\rm{B}'}{ε_\rm{r}C}}\)
∴ Q A ' = \(\large{\frac{Q_\rm{B}'}{ε_\rm{r}}}\) ……⑥
そして、2つのコンデンサーの電荷の総量は他に逃げ所が無いので Q のままであり、つまり、
Q A ' + Q B ' = Q ……⑦
です。⑥式をこれに代入して、
\(\large{\frac{Q_\rm{B}'}{ε_\rm{r}}}\) + Q B ' = Q
∴ \(\large{\frac{1+ε_\rm{r}}{ε_\rm{r}}}\)Q B ' = Q
∴ Q B ' = \(\large{\frac{ε_\rm{r}}{ε_\rm{r}+1}}\)Q
⑦式に入れ戻して、
Q A ' + \(\large{\frac{ε_\rm{r}}{ε_\rm{r}+1}}\)Q = Q
∴ Q A ' = Q - \(\large{\frac{ε_\rm{r}}{ε_\rm{r}+1}}\)Q
= \(\large{\frac{ε_\rm{r}+1-ε_\rm{r}}{ε_\rm{r}+1}}\)Q
= \(\large{\frac{1}{ε_\rm{r}+1}}\)Q
これらの値はよく見ると問2で求めた値
Q A = \(\large{\frac{ε_r}{ε_r+1}}\)Q ……⑧
Q B = \(\large{\frac{1}{ε_r+1}}\)Q ……⑨
と逆になっています。回路においてスイッチを操作した結果、Q A ' = Q B 、Q B ' = Q A となったのです。
各コンデンサーの静電エネルギー( U = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{Q^2}{C}}\) )は
U A ' = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{{Q_\rm{A}}'}^2}{C_\rm{A}}}\) = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{B}}^2}{C}}\)
U B ' = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{{Q_\rm{B}}'}^2}{C_\rm{B}}}\) = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{A}}^2}{ε_rC}}\)
であり、スイッチSを閉じる前の各コンデンサーの静電エネルギーは(問3で求めた静電エネルギーの x = a の場合のことですが)、
U A = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{A}}^2}{C_\rm{A}}}\) = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{A}}^2}{C}}\)
U B = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{B}}^2}{C_\rm{B}}}\) = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{B}}^2}{ε_rC}}\)
です。よって静電エネルギーの減少分は
(U A + U B ) - (U A ' + U B ')
= \(\big(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{A}}^2}{C}}\) + \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{B}}^2}{ε_rC}})\) - \(\big(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{B}}^2}{C}}\) + \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{Q_\rm{A}}^2}{ε_rC}})\)
= \(\large{\frac{1}{2C}}\)⋅\(\big(\)Q A 2 + \(\large{\frac{{Q_\rm{B}}^2}{ε_r}}\) - Q B 2 - \(\large{\frac{{Q_\rm{A}}^2}{ε_r}})\)
= \(\large{\frac{1}{2C}}\)⋅\(\big(\)Q A 2 - \(\large{\frac{{Q_\rm{A}}^2}{ε_r}}\) - Q B 2 + \(\large{\frac{{Q_\rm{B}}^2}{ε_r}})\)
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\big(\)1 - \(\large{\frac{1}{ε_r}})\)Q A 2 - \(\big(\)1 - \(\large{\frac{1}{ε_r}})\)Q B 2 \(\Big\}\)
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\big(\)1 - \(\large{\frac{1}{ε_r}})\)\(\big(\)Q A 2 - Q B 2 \(\big)\Big\}\)
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\big(\)\(\large{\frac{ε_r-1}{ε_r}})\)\(\big(\)Q A 2 - Q B 2 \(\big)\Big\}\)
⑧式、⑨式を代入して、
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\big(\)\(\large{\frac{ε_r-1}{ε_r}})\)\(\big(\)\(\large{\frac{{ε_r}^2}{(ε_r+1)^2}}\)Q 2 - \(\large{\frac{1^2}{(ε_r+1)^2}}\)Q 2 \(\big)\Big\}\)
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\big(\)\(\large{\frac{ε_r-1}{ε_r}})\large{\frac{({ε_r}^2-1)}{(ε_r+1)^2}}\)\(Q^2\Big\}\)
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\)\(\large{\frac{ε_r-1}{ε_r}}⋅\large{\frac{(ε_r+1)(ε_r-1)}{(ε_r+1)^2}}\)\(Q^2\)\(\Big\}\)
= \(\large{\frac{1}{2C}}\)⋅\(\Big\{\large{\frac{(ε_r-1)^2}{ε_r(ε_r+1)}}\)\(Q^2\)\(\Big\}\)
= \(\)\(\large{\frac{(ε_r-1)^2Q^2}{2ε_r(ε_r+1)C}}\)\(\)
電気量の総量が一定だからといって静電エネルギーの総量も一定であるわけではありません。静電エネルギー は電気量と電圧を掛けたもの*
U = \(\large{\frac{1}{2}}\)QV = \(\large{\frac{1}{2}}\)CV 2 = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{Q^2}{C}}\)
閉じる
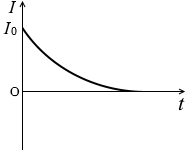
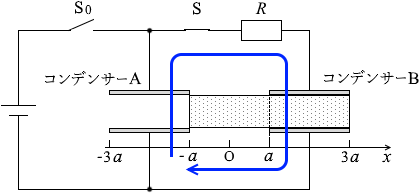 そして、その大きさ(スイッチを閉じた直後の電流の大きさ I0)を求めるために
そして、その大きさ(スイッチを閉じた直後の電流の大きさ I0)を求めるために スイッチを閉じた直後は勢い良く電荷が移動して行きますが、電荷が移動するにつれてAの電圧は下がり、Bの電圧は上がるので、その勢いは徐々に落ちていき(変化量は小さくなり)、やがてA、Bの電圧が等しくなり、電流は止まります。よって電流の時間変化は以下のようになります。
スイッチを閉じた直後は勢い良く電荷が移動して行きますが、電荷が移動するにつれてAの電圧は下がり、Bの電圧は上がるので、その勢いは徐々に落ちていき(変化量は小さくなり)、やがてA、Bの電圧が等しくなり、電流は止まります。よって電流の時間変化は以下のようになります。