導体⋅誘電体を挟んだコンデンサー

前項の法則からいえること

コンデンサーは横方向に分割できる

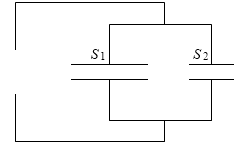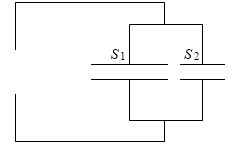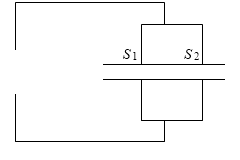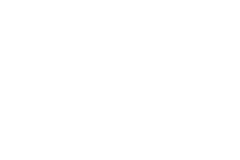『コンデンサーの並列接続』で、複数のコンデンサーを並列に接続した場合の合成容量は、各々のコンデンサーの電気容量を足せばいい C = C₁ + C₂ 、と説明しましたが、

これはつまり逆に、

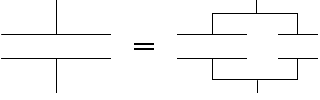コンデンサーの電気容量は横方向に分割しても同じ、ということです。

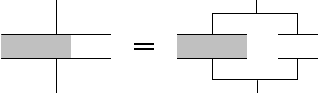またその前提として、誘電率と極板間隔が共通である、とも説明したのですが、実は誘電率は共通でなくても分割できます。

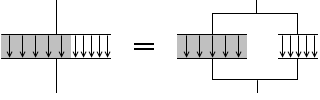平行板コンデンサーでは電気力線の方向が極板に垂直だからです。

誘電体を挟んだグレーの部分の電気力線の本数が少ないのは、誘電体が電場を弱めるからです。電気力線の本数が少ないと電気容量が小さくなるというわけではありません。逆です。誘電体が差し込まれると電気力線は減り電気容量は大きくなります。

コンデンサーは縦方向に分割できる

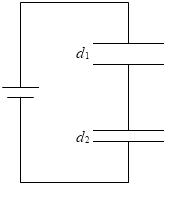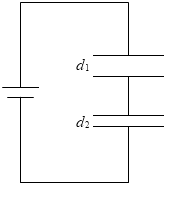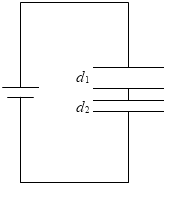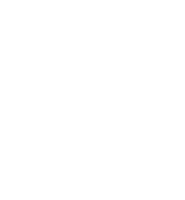『コンデンサーの直列接続』で、複数のコンデンサーを直列に接続した場合の合成容量は、それぞれの極板間の大きさを足し合わせたもの、と説明しましたが、

これはつまり逆に、

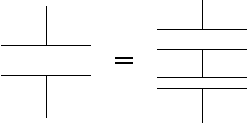コンデンサーの電気容量は、縦方向に分割しても同じ、ということです。

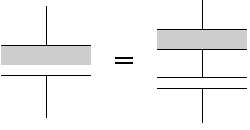またその前提として、誘電率と極板面積が共通である、とも説明したのですが、実は誘電率は共通でなくても分割できます。

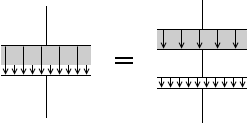極板間に挟む誘電体が直方体で極板の形と同じならば、電気力線の形が変わらないので分割できます。

コンデンサーは順序を変えられる

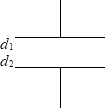このコンデンサーの電気容量と、 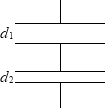これらのコンデンサーの合成容量が同じで、

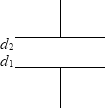このコンデンサーの電気容量と、 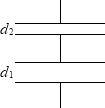これらのコンデンサーの合成容量が同じであるのだから、

これらのコンデンサーと、 これらのコンデンサーの合成容量は同じです。

つまりコンデンサーは順序を変えられます。これは３つ以上のときでも成り立ちます。

導体を挟んだコンデンサー

このコンデンサーと、 これらのコンデンサーの合成容量は同じであるわけですが、このとき、

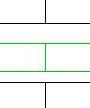この緑の部分の導線の材質は導体で出来ています。そしてこの部分の形は、

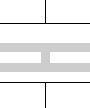このような形であったとしても、合成容量は変わりません。

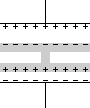電荷はコンデンサーの極板と対面する部分にしか存在しません。極板と向かい合う面の形が極板と鏡写しの形になっていれば合成容量は変わりません。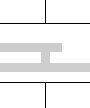＊ このような形だったりするとまずいです。
　閉じる

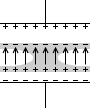途中部分の形がどうなっていようと電気力線の形は変わりません。＊さすがに 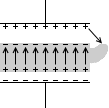このような形だったりすると余計な電気力線が発生して、電気容量は狂ってしまうと思います。
　閉じる

さらに、このような形だったとしても、合成容量は変わりません。

つまり、 この形をした導体を挟んだ このコンデンサーと、 このコンデンサーは電気容量が同じです。

コンデンサーに”導体”を挟んだ場合は、導体部分が圧縮されて無くなった とみなすことができるということです。

電気容量 C₀ 、誘電率 ε₀ ＊ε₀ というのは真空、あるいは空気の誘電率です。つまり極板間に何も挟まれてないときの誘電率です。
　閉じる、極板面積 S 、極板間隔 d の平行板コンデンサーの極板の間に、

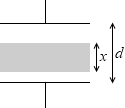面積が極板と同じ S で、厚さが極板間隔より薄い x の導体板を挟んだとします。

このときの電気容量 C は、極板間が d-x になったと考えればいいわけですから、

　　　　C = ε₀\(\large{\frac{S}{d-x}}\)

これを何も挟まないときの電気容量 C₀ = ε\(\large{\frac{S}{d}}\) と比べますと、

　　　　C = ε₀\(\large{\frac{S}{d-x}}\) = \(\large{\frac{d}{d}}\)ε₀\(\large{\frac{S}{d-x}}\)

　　　　　 = \(\large{\frac{d}{d-x}}\)ε₀\(\large{\frac{S}{d}}\)

　　　　　 = \(\large{\frac{d}{d-x}}\)C₀

となります。

コンデンサーに導体を挟むと、極板間が小さくなったのと同等とみなすことができ、電気容量は大きくなります。

誘電体を挟んだコンデンサー

次に、誘電体（不導体）を挟んだ場合について考えてみます。

上で説明したようにコンデンサーは縦方向に分割できるので、

誘電体を挟んだ 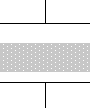このようなコンデンサーは、 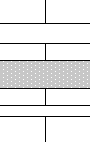このように分割できます。

さらに、コンデンサーは順序を変えられるので、

このように変えられます。

そして、コンデンサーは合体することができるので、

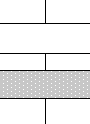このようにすることができます。

つまり、 このようなコンデンサーの電気容量は、 これらのコンデンサーの合成容量と同じということです。

コンデンサーに”誘電体”を挟んだ場合は、２つのコンデンサーを直列に接続したとみなすことができるということです。

電気容量 C₀ 、誘電率 ε₀ 、極板面積 S 、極板間隔 d の平行板コンデンサーの極板の間に、

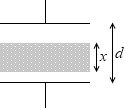面積が極板と同じ S で、厚さが極板間隔より薄い x の誘電体の板を挟んだとします。

このコンデンサーの電気容量 C は、

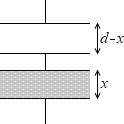左図のような２つのコンデンサーの合成容量と同じであるわけです。

上のコンデンサーの電気容量を C₁ としますと、C₁ = ε₀\(\large{\frac{S}{d-x}}\)

下のコンデンサーの電気容量を C₂ 、誘電体の比誘電率を ε_r としますと、C₂ = ε_rε₀\(\large{\frac{S}{x}}\) 。

よって、直列接続の合成容量の逆数はそれぞれの逆数の和だから、

　　　　\(\large{\frac{1}{C}}\) = \(\large{\frac{1}{C_1}}\)+\(\large{\frac{1}{C_2}}\) = \(\large{\frac{d-x}{ε_0 S}}\)+\(\large{\frac{x}{ε_r ε_0 S}}\) = \(\large{\frac{ε_r (d-x)}{ε_r ε_0 S}}\)+\(\large{\frac{x}{ε_r ε_0 S}}\) = \(\large{\frac{ε_r (d-x)+x}{ε_r ε_0 S}}\)

　∴　　C = \(\large{\frac{ε_r ε_0 S}{ε_r (d-x)+x}}\)

これを何も挟まないときの電気容量 C₀ = ε₀\(\large{\frac{S}{d}}\) と比べますと、

　　　　C = \(\large{\frac{ε_r ε_0 S}{ε_r (d-x)+x}}\) = \(\large{\frac{ε_r ε_0 S}{ε_r (d-x)+x}\frac{d}{d}}\)

　　　　　 = \(\large{\frac{ε_r d}{ε_r (d-x)+x}}\)ε₀\(\large{\frac{S}{d}}\)

　　　　　 = \(\large{\frac{ε_r d}{ε_r (d-x)+x}}\)C₀　　　……①

となります。しかしこれでは式が複雑過ぎて C と C₀ はどちらが大きいのかよく分かりません。

\(\large{\frac{ε_r d}{ε_r (d-x)+x}}\) が 1 より大きいかどうか考えてみます。

まず、比誘電率というものは 1 より大きいので、

　　　　ε_r > 1　　　　この式の両辺に x を掛けますと、x > 0 ですので、

　　　　ε_rx > x　　　　移項しますと、

　　　　0 > - ε_rx + x　　　　両辺に ε_rd を加えますと、

　　　　ε_rd > ε_rd - ε_rx + x　　　　整理しますと、

　　　　ε_rd > ε_r (d - x) + x　　　　両辺を ε_r (d - x) + x で割りますと、

　　　　\(\large{\frac{ε_r d}{ε_r (d-x)+x}}\) > 1

というわけで \(\large{\frac{ε_r d}{ε_r (d-x)+x}}\) が 1 より大きいということが分かり、C は C₀ より大きいということが分かり、コンデンサーに誘電体を挟むと電気容量が大きくなる、ということが分かります。

もし x = d であった場合は、①式に代入して、

　　　　C = \(\large{\frac{ε_r d}{ε_r (d-x)+x}}\)C₀ = \(\large{\frac{ε_r d}{ε_r (d-d)+d}}\)C₀ = \(\large{\frac{ε_r d}{d}}\)C₀ = ε_rC₀

となり、『比誘電率』の⑥式と一致します。

どちらを挟んでも電気容量が大きくなる

コンデンサーは、”導体”と”誘電体”のどちらを挟んでも電気容量が大きくなります。（導体を挟む場合は極板間のすべてを埋め尽くさない場合です。極板間すべてを導体で埋め尽くしたらそれはコンデンサーではありません）

複雑な問題

ここまで説明してきたように考えますと、複雑な電気容量の問題が出題されても簡単に解くことができます。

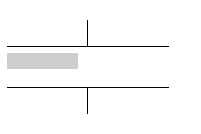左図のようなコンデンサーに、直方体の物体が挿入されたときの電気容量を求めよ、という問題が出題された場合、

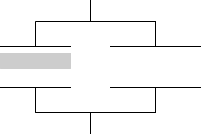まず、横に分割し、

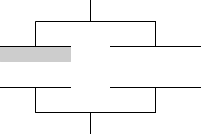物体を端に寄せ（これは上で説明した『順序を変える』ことに相当します）、

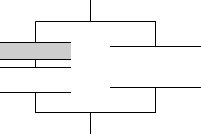縦に分割すれば合成容量を求められます。

（分割する順序については、先に縦に分割してから次に横に分割してもいいです。）

挿入した物体の材質が導体なら「無い」ものとみなし、誘電体なら比誘電率を掛けます。

求めた合成容量は、元の何も挿入してない場合の電気容量より必ず大きくなります。