qHBA4　■わかりやすい高校物理の部屋■

図3のように、真空中で荷電粒子（イオン）を加速する円型の装置を考える。この装置には、内部が中空で半円型の二つの電極が水平に向かい合わせて設置され、それらの間に電圧をかけることができる。全体に一様で一定な磁束密度 B の磁場が鉛直下向きにかかっている。
質量 m 、正電荷 q をもつ粒子が、点Pから入射され、中空電極内では磁場による力のみを受けて円運動を行い、半周ごとに電極間を通過する。電極間の電場の向きは粒子が半周するたびに反転して、電極間を通過する粒子は、大きさ V の電圧で常に加速されるものとする。

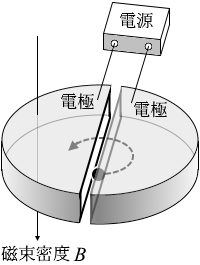
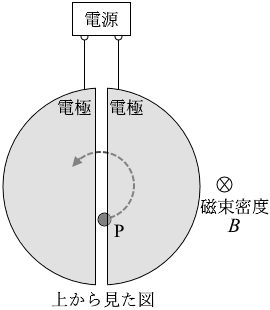
（問3）運動エネルギー E₀ をもつ粒子が電極内に入射し、電極間を n 回通過した。粒子のもつ運動エネルギーを式で表わせ。

（問4）粒子が電極間を n 回通過した後の運動エネルギーを E_n とする。そのときの速さ v と円運動の半径 r を表す式の組合せとして正しいものを、次の①～⑥のうちから一つ選べ。

	速さ `v`	円運動の半径 `r`
①	\(\sqrt{\frac{2E_n}{m}}\)	\(\large{\frac{mv}{qB}}\)
②	\(\sqrt{\frac{2E_n}{m}}\)	\(\large{\frac{mB}{qv}}\)
③	\(\sqrt{\frac{2E_n}{m}}\)	\(\large{\frac{qvB}{m}}\)
④	\(\large{\frac{E_n}{m}}\)	\(\large{\frac{mv}{qB}}\)
⑤	\(\large{\frac{E_n}{m}}\)	\(\large{\frac{mB}{qv}}\)
⑥	\(\large{\frac{E_n}{m}}\)	\(\large{\frac{qvB}{m}}\)

#センター15本試物理

（問3）
『電位』項で説明したように、q の電荷が電位差（電圧）V の間を運ばれると qV の運動エネルギーを得ます。（重力による位置エネルギーに例えると、h の高さから落とされて mgh だけ運動エネルギーが増した、となります）。それを n 回繰り返したので n × qV の運動エネルギーを得たことになります。始めの運動エネルギーが E₀ であるので粒子が n 回通過した後の運動エネルギーは

　　　　 nqV + E₀

となります。

（問4）
E_n は運動エネルギーであるので、 \(\large{\frac{1}{2}}\)mv² とも表現でき、すなわち、

　　　　\(\large{\frac{1}{2}}\)mv² = E_n

　∴　　v² = \(\large{\frac{2E_n}{m}}\)

　∴　　 v = \(\sqrt{\frac{2E_n}{m}}\)

さらに、磁場中を周回する荷電粒子の円運動の運動方程式を立てますと、

　　　　m\(\large{\frac{v^2}{r}}\) = qvB

　∴　　m\(\large{\frac{v}{r}}\) = qB

　∴　　 r = \(\large{\frac{mv}{qB}}\)

答えは ① です。