磁場中の荷電粒子の運動

磁場に垂直に入射した荷電粒子の運動

一様な磁場の中に垂直に荷電粒子を放り込む

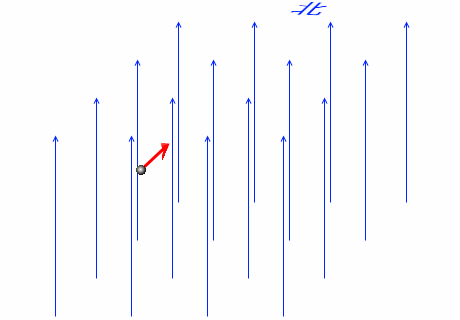鉛直上向きの一様な磁場があり、その中に荷電粒子が放り込まれたとします。そのときの初速の向きが北向きであるとします。

この荷電粒子の電気量は正であるとします。もし荷電粒子の電気量が負（たとえば電子）の場合は進む向きを逆向きとして考えます。（電子が北に向かうなら正電荷が南に向かうとみなし、電子が南に向かうなら正電荷が北に向かうとみなして、ローレンツ力の向きを考えます）。

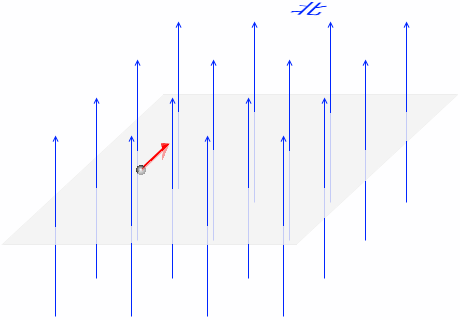この初速の向きは、水平面内（磁場に対して垂直）の北向きであるとします。

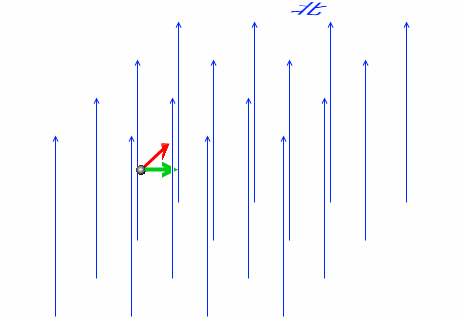磁場中で運動する荷電粒子はローレンツ力を受けます。その方向はフレミングの左手の法則にのっとった方向であり、今の場合、東向きです。

ですから、北に向かおうとした荷電粒子はちょっと東へ進路を変えます。

このとき、緑矢印は赤矢印の方向を変えますが、赤矢印の長さ（荷電粒子の速さ）には影響を与えません。緑矢印と赤矢印が垂直だからです。

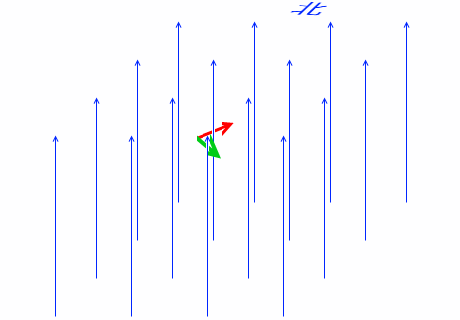進んでいく荷電粒子にはそのままローレンツ力が掛かり続け、その力の方向はフレミングの左手の法則により、今度は南東の方向になります。そしてその力によってまた進路が変わっていきます。

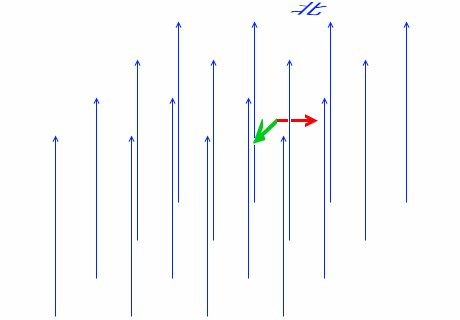さらに進んでいって荷電粒子が東に向くと、ローレンツ力の向きは南向きになります。

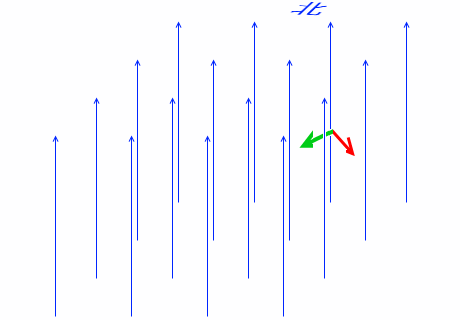さらに進んでいくと、ローレンツ力の向きは南西になります。

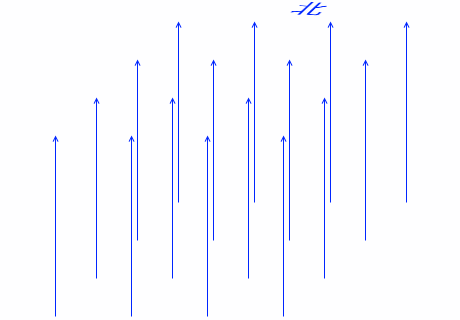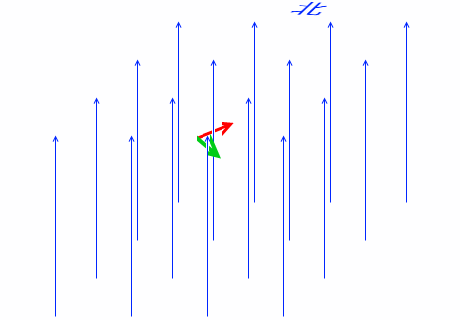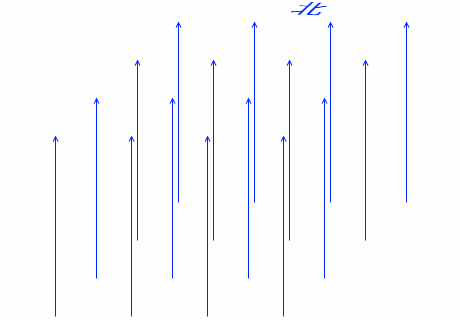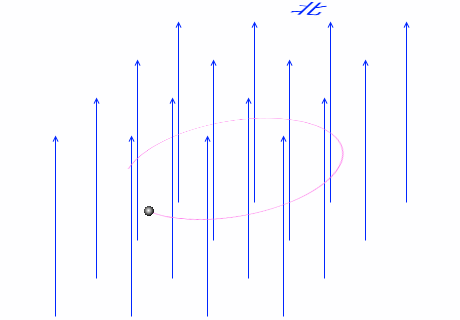このようにして結局、荷電粒子は円を描きます。

ローレンツ力というものが常に進行方向に対して垂直にはたらくというのがポイントです。

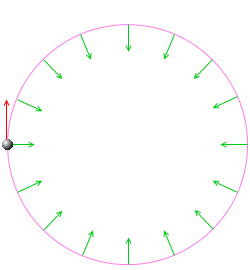進行方向に対して常に垂直に一定の大きさの力を受ける物体の軌道は必ず円になります。「常に垂直で一定」なら必ず円になります。元の位置に戻ってきます。（いまは重力は無視しています）。重力が無く、一様な磁場があるところに荷電粒子を垂直に放り込むと円運動を起こすのです。与えられた初速を保ちながら等速円運動をします。ローレンツ力が向心力となっています。このような運動をサイクロトロン運動といいます。

荷電粒子というものは磁場を横切るとき、まっすぐ飛ぶことができず、どうしても旋回してしまいます。

磁場中を周回する荷電粒子の円運動の運動方程式

磁束密度を B [T] 、荷電粒子の質量を m [kg] 、与えられた初速を v [m/s] 、円運動の半径を r [m] とします。

すると、ローレンツ力 f [N] は、

　　　　f = qvBsinθ

ですが、今は v と B が垂直 θ=90° なので sinθ=1 。つまり、

　　　　f = qvB

です。そして、質量 m 、速さ v 、半径 r で等速円運動しているときの向心力 F は、

　　　　F = m\(\large{\frac{v^2}{r}}\)

です。ローレンツ力 f がこの向心力 F になっているのだから、

　　　　m\(\large{\frac{v^2}{r}}\) = qvB　　……①

です。

比電荷

①式は以下のように変形できます。

　　　　m\(\large{\frac{v}{r}}\) = qB

　　∴　\(\large{\frac{v}{Br}}\) = \(\large{\frac{q}{m}}\)

　　∴　\(\large{\frac{q}{m}}\) = \(\large{\frac{v}{Br}}\)

左辺の \(\large{\frac{q}{m}}\) は荷電粒子の電気量と質量の比を表しています。これを比電荷といいます。右辺は磁場の大きさと運動の様子を示しています。ものすごく小さい粒子はその質量を測定するのが困難ですが、運動の様子を測定することでその粒子の質量が推定できます。

電子の比電荷は約 -1.759×10¹¹C/kg です。

円運動の半径と周期

①式から半径 r を求めてみますと、

　　　　m\(\large{\frac{v}{r}}\) = qB

　　∴　\(\large{\frac{mv}{qB}}\) = r

　　∴　r = \(\large{\frac{mv}{qB}}\)　　……②

次に、周期 T [s] を求めてみます。周期というのは、1周の長さ 2πr [m] を、周回する速さ v [m/s] で割ったものだから、＊T = \(\large{\frac{2\pi}{ω}}\)　に　v = rω　を代入する、と考えてもいいです。
　閉じる

　　　　T = \(\large{\frac{2\pi r}{v}}\)　　……③

この式に②式を代入すると、

　　　　T = \(\large{\frac{2\pi m}{qB}}\)　　……④

となります。

③式を見ると、周期 T は速度 v によって決まるように感じてしまいますが、②式により v が変動すると r も変動するので、そうもいかないことが分かります。初速が大きいと軌道半径も大きいのです。

④式は、周期 T は比電荷 \(\large{\frac{q}{m}}\) と磁束密度 B によって決まるということを示しています。荷電粒子が電子であった場合、その比電荷が分かっているので、周期は磁束密度の大きさだけで決まります。

磁場に斜めに入射した荷電粒子の運動

一様な磁場の中に斜めに荷電粒子を放り込む

次に、磁場に対して垂直ではなく斜めに荷電粒子を放り込む場合を考えてみます。

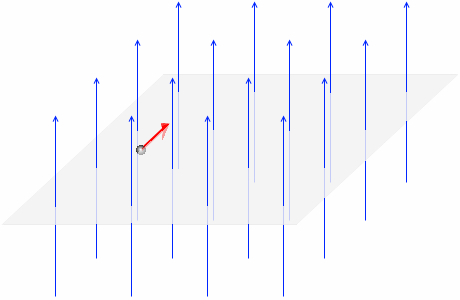このような向きではなく、

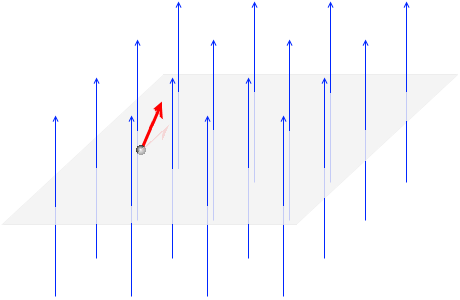このような向きということです。

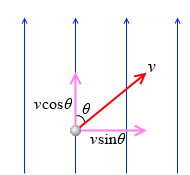速度 v を、磁場に平行な成分 vcosθ と磁場に垂直な成分 vsinθ に分解して考えます。

θ は磁場と速度のなす角です。

磁場に平行な成分 vcosθ

磁場に平行な成分 vcosθ は磁場からローレンツ力を受けません。荷電粒子の進む方向と磁場の方向が同じ場合はローレンツ力が発生しません＊ローレンツ力の式 f = qvBsinθ の sinθ は垂直（θ=90°）のとき sinθ=1 となりますが、平行（θ=0）のとき sinθ=0 となり、これは f = qvBsinθ = 0 ということです。ローレンツ力が 0 ということです。
　閉じる。力を受けないということは等速直線運動を続けるということです。初速が保たれるということです。磁場に平行な成分 vcosθ はずっとそのままということです。

磁場に垂直な成分 vsinθ

磁場に垂直な成分については、上で説明した『磁場に垂直に入射した荷電粒子の運動』の場合と同じになります。等速円運動です。しかし力の大きさは少し小さくなります。『磁場に垂直に入射した荷電粒子の運動』における v の部分に vsinθ を代入しなければなりません。

ローレンツ力の式と①～④式の v の部分に vsinθ を代入すると、

　　　　f = qvBsinθ

　　　　m\(\large{\frac{(v\sin\theta)^2}{r}}\) = qvBsinθ　　……①'　（← m\(\large{\frac{v^2}{r}}\) = qvB）

　　　　r = \(\large{\frac{mv\sin\theta}{qB}}\)　　……②'　（← r = \(\large{\frac{mv}{qB}}\)）

　　　　T = \(\large{\frac{2\pi r}{v\sin\theta}}\)　　……③'　（← T = \(\large{\frac{2\pi r}{v}}\)）

　　　　T = \(\large{\frac{2\pi m}{qB}}\)　　……④　（← T = \(\large{\frac{2\pi m}{qB}}\)）

となります。④式には v が含まれていないので書き換えられません。このことは、周期 T は入射角によらないということを意味しています。磁場に対して垂直に入射しようが斜めに入射しようが周期は変わらないということです。（周回半径については斜めのときの方が小さくなります）。上で説明したように周期 T は速度 v には依存せず、比電荷 \(\large{\frac{q}{m}}\) に依存します。

上記５つの式において sinθ=1 のときに相当するのが『磁場に垂直に入射した荷電粒子の運動』である、という見方もできます。（このとき vcosθ=0 です。sinθ=1 のときは cosθ=0 です。）

らせん運動

平行成分が等速直線運動で、垂直成分が等速円運動ということはそれは合成すると、らせん運動になります。

荷電粒子を磁場の中に放り込むとき、ちょうどうまく垂直に放り込むのは難しく、たいてい斜めになってしまいますが、そうすると荷電粒子は磁場の中でらせん運動を始めるということです。

垂直方向に1周する間に、平行方向にどのくらいの距離進むか考えてみますと、それは、平行成分速度 vcosθ に、1周する時間、すなわち T を掛けたものです。この距離のことをピッチといいます。 l で表しますと、

　　　　l = vcosθ × T

　　　　 = vcosθ × \(\large{\frac{2\pi m}{qB}}\)

　　　　 = \(\large{\frac{2\pi mv\cos\theta}{qB}}\)

となります。