(問1)
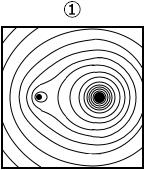
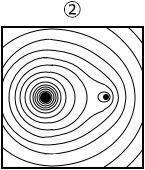
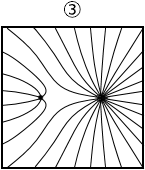
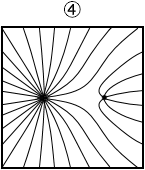
電気力線は電荷から湧き出すもので、等電位線は電荷を同心円上にくるむものです。ですから、正解は①か②のどちらかです。
そして、等電位線は密なところは電場が強くなっているものですし、Q の方が \(\large{\frac{Q}{4}}\) より、電位が高くなっているはずであり、そのことを示している図は ② です。(地図の等高線で考えますと、標高が高くなっているのは左側の山)
(問2)
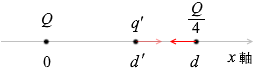
 第3の点電荷の電気量を q' (q'>0)と置きますと、
第3の点電荷の電気量を q' (q'>0)と置きますと、
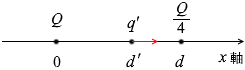 Q の点電荷から受ける静電気力は
Q の点電荷から受ける静電気力は
k\(\large{\frac{Qq'}{d'^2}}\)
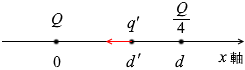 \(\large{\frac{Q}{4}}\) の点電荷から受ける静電気力は
\(\large{\frac{Q}{4}}\) の点電荷から受ける静電気力は
k\(\large{\frac{\frac{Q}{4}q'}{(d-d')^2}}\)
この2つの静電気力の合力が 0 なのだから、
k\(\large{\frac{Qq'}{d'^2}}\) = k\(\large{\frac{\frac{Q}{4}q'}{(d-d')^2}}\)
∴ \(\large{\frac{1}{d'^2}}\) = \(\large{\frac{\frac{1}{4}}{(d-d')^2}}\)
∴ 4(d - d')2 = d'2
∴ 4(d2 - 2dd' + d'2) = d'2
∴ 4d2 - 8dd' + 4d'2 = d'2
∴ 4d2 - 8dd' + 3d'2 = 0
∴ 3d'2 - 8dd' + 4d2 = 0
∴ (3d' - 2d)(d' - 2d) = 0
高校数学の因数分解です。
3d'2 - 8dd' + 4d2 について、
掛けて3、掛けて4になる組合せは
(3 4)
(1 1)
あるいは
(3 2)
(1 2)
で、
この2つのうち、たすき掛けの和が8になるのは
(3 2)
(1 2)
です。
3×2+1×2=8 です。
3×1+1×4 では 8 になりません。
というわけで、
(3d' - 2d)(d' - 2d)
です。
∴ d' = \(\large{\frac{2}{3}}\)d、2d
このうち 2d は力の向きが同じになってしまいますし、問題文で、Q の点電荷と \(\large{\frac{Q}{4}}\) の点電荷の間、と指定されているので、
答えは ④ \(\large{\frac{2}{3}}\)d です。
(余談)
なお、q' は計算途中で消えてしまっていて、これはつまり、無関係ということです。q' がどんな大きさでも、正でも負でも、x = \(\large{\frac{2}{3}}\)d の位置にありさえすれば、静電気力の合力は 0 になります。
そして、x = \(\large{\frac{2}{3}}\)d ということは、Q の点電荷からの距離が \(\large{\frac{Q}{4}}\) の点電荷からの距離の2倍ということであり、これは静電気力の式
F = k\(\large{\frac{q_1q_2}{r^2}}\)
が距離の2乗に反比例していることに依ります。震源の力が4倍であれば、2倍の距離、離れていればつり合いがとれます。このように考えると、この問題は暗算で解くことができます。
問題設定が「Q」 と 「\(\large{\frac{Q}{9}}\)」 であれば、3倍の距離の差がでる位置が答えであり、
d' = \(\large{\frac{3}{4}}\)d
と暗算で導き出せます。
クーロンの法則
F = k\(\large{\frac{q_1q_2}{r^2}}\)
というものは、2つの電荷 q1 、q2 があるときに、
 それぞれの電荷にはたらく力の大きさを表しています。(斥力の場合)
それぞれの電荷にはたらく力の大きさを表しています。(斥力の場合)
 引力の場合ならこうです。
引力の場合ならこうです。
2本の矢印のそれぞれの長さが k\(\large{\frac{q_1q_2}{r^2}}\) であるということです。同じ大きさで、必ず対になっています。作用反作用の法則です。
というわけで、\(\large{\frac{Q}{4}}\) の点電荷になんらかの静電気力がはたらいていれば、それと対をなす力がどこかにはたらいているはずです。しかしそのような力はありません。Q の点電荷も第3の点電荷も合力が 0 と言っています。対になるべき力が無いのです。
これはつまり、\(\large{\frac{Q}{4}}\) の点電荷にはたらく合力も 0 になっているということです。答えは ① です。
作用反作用の法則をちゃんと理解しているかを問う、いい問題だと思います。
(一つひとつの力を考えてみる)
 \(\large{\frac{Q}{4}}\) は Q から力を受けています。(問題文より Q 、\(\large{\frac{Q}{4}}\) は正であるので、この力は斥力)。その大きさを f とします。
\(\large{\frac{Q}{4}}\) は Q から力を受けています。(問題文より Q 、\(\large{\frac{Q}{4}}\) は正であるので、この力は斥力)。その大きさを f とします。
 その力と対をなす力が Q にはたらいています。
その力と対をなす力が Q にはたらいています。
 Q にはたらく力の合力は 0 であるから、反対向きに f の力がはたらいているはずです。
Q にはたらく力の合力は 0 であるから、反対向きに f の力がはたらいているはずです。
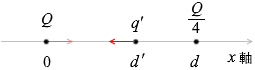 この力は q' にはたらく力と対をなしているはずで、(引力になっているはずで、つまり q' は負)、
この力は q' にはたらく力と対をなしているはずで、(引力になっているはずで、つまり q' は負)、
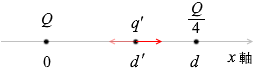 q' にはたらく力の合力は 0 であるから、反対向きに f の力がはたらいているはずで、
q' にはたらく力の合力は 0 であるから、反対向きに f の力がはたらいているはずで、
 この力は \(\large{\frac{Q}{4}}\) にはたらく力と対をなしているはずです。
この力は \(\large{\frac{Q}{4}}\) にはたらく力と対をなしているはずです。
というわけで、
 \(\large{\frac{Q}{4}}\) には、向きが逆で同じ大きさの2つの力がはたらいています。
\(\large{\frac{Q}{4}}\) には、向きが逆で同じ大きさの2つの力がはたらいています。
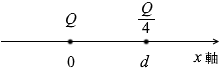
 第3の点電荷の電気量を q' (q'>0)と置きますと、
第3の点電荷の電気量を q' (q'>0)と置きますと、 Q の点電荷から受ける
Q の点電荷から受ける \(\large{\frac{Q}{4}}\) の点電荷から受ける静電気力は
\(\large{\frac{Q}{4}}\) の点電荷から受ける静電気力は それぞれの電荷にはたらく力の大きさを表しています。(斥力の場合)
それぞれの電荷にはたらく力の大きさを表しています。(斥力の場合) 引力の場合ならこうです。
引力の場合ならこうです。 \(\large{\frac{Q}{4}}\) は Q から力を受けています。(問題文より Q 、\(\large{\frac{Q}{4}}\) は正であるので、この力は斥力)。その大きさを
\(\large{\frac{Q}{4}}\) は Q から力を受けています。(問題文より Q 、\(\large{\frac{Q}{4}}\) は正であるので、この力は斥力)。その大きさを  その力と対をなす力が Q にはたらいています。
その力と対をなす力が Q にはたらいています。 Q にはたらく力の合力は 0 であるから、反対向きに
Q にはたらく力の合力は 0 であるから、反対向きに  この力は q' にはたらく力と対をなしているはずで、(引力になっているはずで、つまり q' は負)、
この力は q' にはたらく力と対をなしているはずで、(引力になっているはずで、つまり q' は負)、 q' にはたらく力の合力は 0 であるから、反対向きに
q' にはたらく力の合力は 0 であるから、反対向きに  この力は \(\large{\frac{Q}{4}}\) にはたらく力と対をなしているはずです。
この力は \(\large{\frac{Q}{4}}\) にはたらく力と対をなしているはずです。 \(\large{\frac{Q}{4}}\) には、向きが逆で同じ大きさの2つの力がはたらいています。
\(\large{\frac{Q}{4}}\) には、向きが逆で同じ大きさの2つの力がはたらいています。