等電位面

等電位面

等電位面とは

電場において、電位の等しい地点を結んでできる面を等電位面といいます。

なぜ等電位「線」でなく、等電位「面」なのかといいますと、電場というのは実際には立体的に3次元的に広がっていて、電位の等しい地点を結ぶと「線」ではなく「面」になるからです。

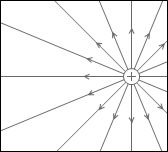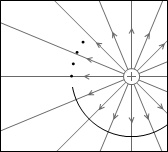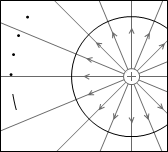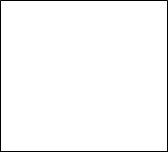
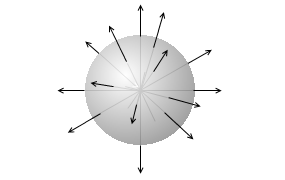たとえば点電荷が作る電場において電位の等しい地点を連ねると球面になります。

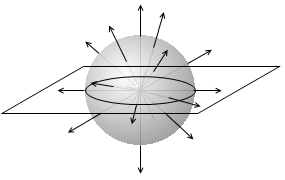これを紙面で表現するときには、平面で切った断面図を表していることになります。このようなときは等電位面のことを等電位線をいうことがあります。

等電位面の例

等電位面の例をいくつか示してみます。黒い線が等電位面で、白い線が電気力線です。

　　　

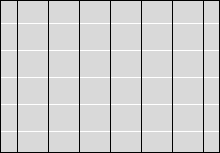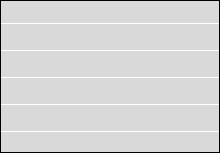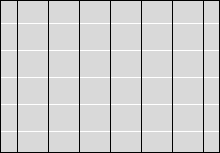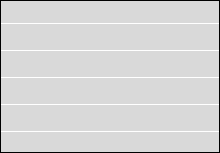
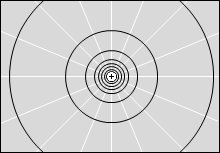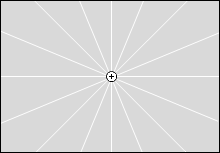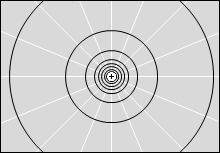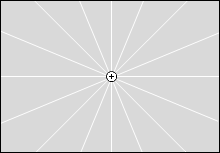
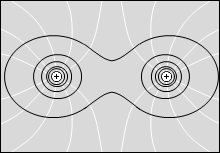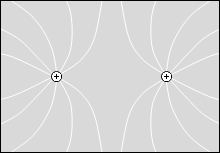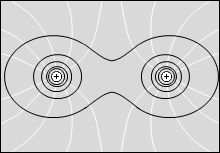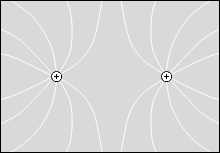
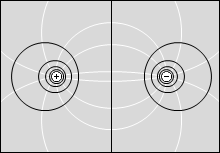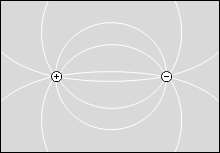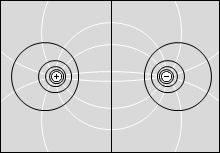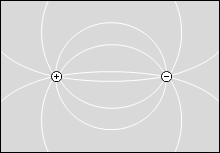
縦軸を電位としたグラフを描きますと以下のようになります。

　　　

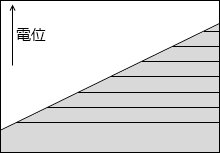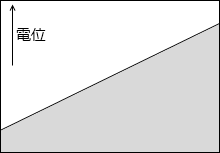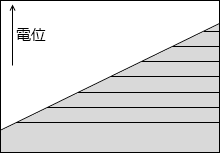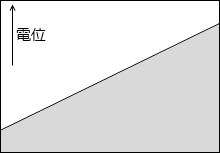
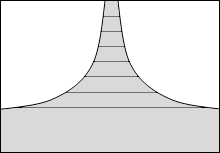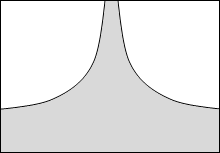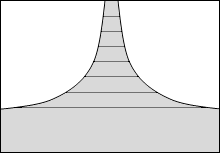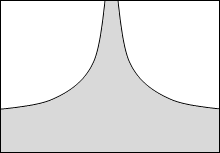
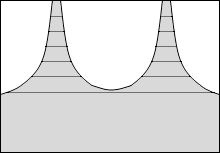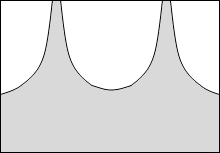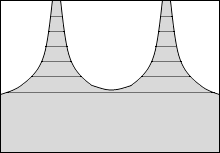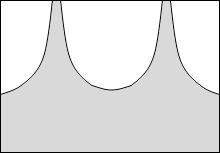
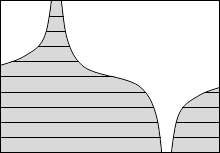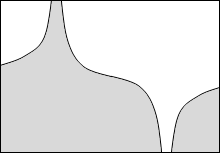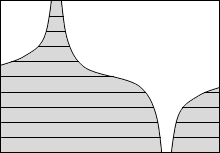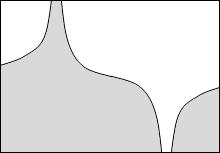
このことから分かると思いますが、等電位面は地図における等高線のようなものです。地図における等高線というものは重力における位置エネルギーの指標になっていますので、等電位面も電位の指標であるといえます。＊ 天気図における等圧線もこれに似ています。

下で説明する「等電位面と電気力線は常に直交する」というのは、
天気図において、等圧線と風の向きが直交すること（厳密には直交しませんが）に似ています。
あるいは、地図において、等高線と水の流れの向きが直交することに似ています。

「等電位面が密なところは電場が強い」というのは、
天気図において、等圧線の間隔が狭いところは風が強いことに似ています。
あるいは、地図において、等高線の間隔が狭いところは急勾配であることに似ています。
　閉じる

等電位面の性質

等電位面には以下のような性質があります。

  • 等電位面と電気力線は常に直交する。
    等電位面に沿って電荷を動かすとき仕事が 0 ということは、その方向には静電気力の成分が 0 ということです。つまり等電位面は電気力線と直交しているということです。静電気力の成分が少しでもあるとすると力が存在するのだから仕事が 0 ではないことになってしまい、上の性質に矛盾するので、静電気力の成分は少しも残ってない、つまり直角、ということです。（『向きが違う例』参照）
    上の性質とこの性質は同じことをいっています。「仕事が 0 」と「直交する」は事実上同じ意味です。
  • 等電位面が密なところは電場が強い。
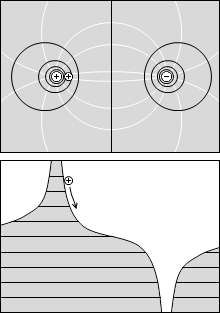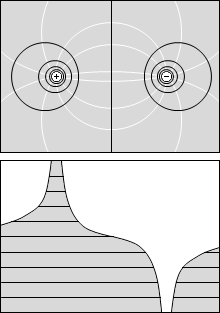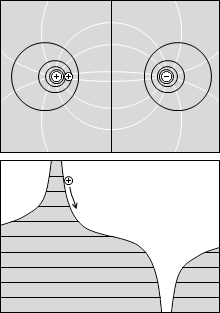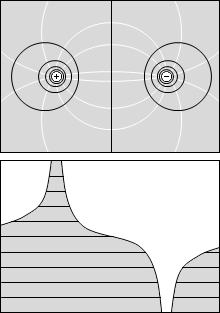
    等電位面の間隔が狭いところは、縦軸を電位としたグラフにおいて曲線の傾きが急になっています。この傾きは電場の大きさを表しています。
    このことは地図における等高線と同じです。
    縦軸を電位としたグラフにおいて、曲線の上に正電荷を置いたとき、転がり落ちる様子を想像してみてください。静電気力を重力にたとえることによって電場の様子が想像しやすくなります。
↑ ↓