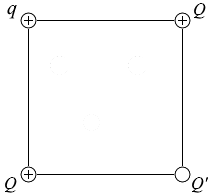
図1のように、正方形の各頂点に四つの点電荷を固定した。それぞれの電気量は q 、Q 、Q' 、Q である。ただし、Q > 0 、q > 0 である。電気量 q の点電荷にはたらく静電気力がつり合うとき、Q' を表す式として正しいものを、下の①~⑧のうちから一つ選べ。
① Q ② \(\sqrt{2}\)Q ③ 2Q ④ 2\(\sqrt{2}\)Q ⑤ - Q ⑥ - \(\sqrt{2}\)Q ⑦ - 2Q ⑧ - 2\(\sqrt{2}\)Q
#センター15本試物理
図1のように、正方形の各頂点に四つの点電荷を固定した。それぞれの電気量は q 、Q 、Q' 、Q である。ただし、Q > 0 、q > 0 である。電気量 q の点電荷にはたらく静電気力がつり合うとき、Q' を表す式として正しいものを、下の①~⑧のうちから一つ選べ。

① Q ② \(\sqrt{2}\)Q ③ 2Q ④ 2\(\sqrt{2}\)Q ⑤ - Q ⑥ - \(\sqrt{2}\)Q ⑦ - 2Q ⑧ - 2\(\sqrt{2}\)Q
#センター15本試物理
正方形の一辺の長さを l としますと、
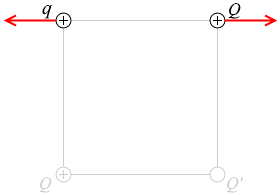 左上の q と右上の Q は k\(\large{\frac{qQ}{l^2}}\) (k は比例定数。『静電気力』項参照)の力で反発し合ってます。
左上の q と右上の Q は k\(\large{\frac{qQ}{l^2}}\) (k は比例定数。『静電気力』項参照)の力で反発し合ってます。
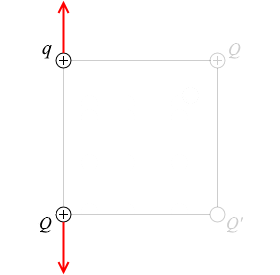 同様に、左上の q と左下の Q は k\(\large{\frac{qQ}{l^2}}\) の力で反発し合ってます。
同様に、左上の q と左下の Q は k\(\large{\frac{qQ}{l^2}}\) の力で反発し合ってます。
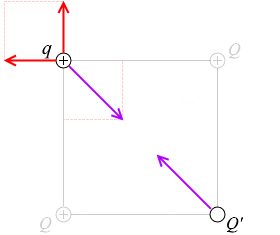 q の点電荷にはたらく静電気力がつり合っているときは、左図の紫矢印のような静電気力が左下の Q' との間にはたらいているはずであり、この力の正負は(引力だから)負であり、その大きさは(三角比より) k\(\large{\frac{qQ}{l^2}}\) の \(\sqrt{2}\)倍のはずです。
q の点電荷にはたらく静電気力がつり合っているときは、左図の紫矢印のような静電気力が左下の Q' との間にはたらいているはずであり、この力の正負は(引力だから)負であり、その大きさは(三角比より) k\(\large{\frac{qQ}{l^2}}\) の \(\sqrt{2}\)倍のはずです。
q と Q' の間の静電気力は
k\(\large{\frac{qQ'}{(\sqrt{2}l)^2}}\)
と表せますので、
k\(\large{\frac{qQ'}{(\sqrt{2}l)^2}}\) = - \(\sqrt{2}\) × k\(\large{\frac{qQ}{l^2}}\)
∴ \(\large{\frac{Q'}{2}}\) = - \(\sqrt{2}\)Q
∴ Q' = - 2\(\sqrt{2}\)Q
答えは ⑧ です。