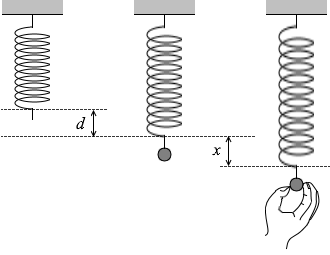
図1のように、上端を固定したばね定数 k のばねの下端におもりをつるしたところ、ばねが自然の長さから d だけ伸びた状態で静止した。このおもりを、手でさらに x だけ引き下げ、静止させた。このとき、手がおもりを引いている力の大きさ F はいくらか。ただし、ばねの質量は無視できるものとする。
#センター10本試
図1のように、上端を固定したばね定数 k のばねの下端におもりをつるしたところ、ばねが自然の長さから d だけ伸びた状態で静止した。このおもりを、手でさらに x だけ引き下げ、静止させた。このとき、手がおもりを引いている力の大きさ F はいくらか。ただし、ばねの質量は無視できるものとする。
#センター10本試
『鉛直ばね振り子の力学的エネルギー』を読んでもらえばすぐに
F = kx
と分かると思います。
一応説明しますと、
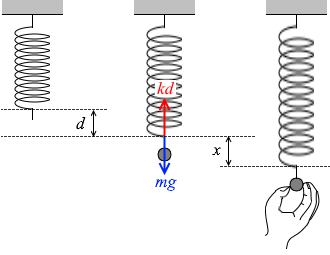d だけ伸びたばねは、 kd の力で上に引っ張っています。そこにおもりがつるされてつり合っています。おもりの質量を m としますと、重力は mg です。つまり、
kd = mg ……①
が成り立っています。
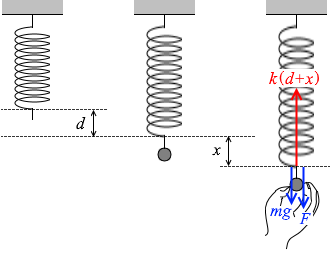d+x だけ伸びたばねは、 k(d+x) の力で上に引っ張っています。そこにおもりがつるされ、かつ、F で下に引っ張ってつり合っています。つまり、
k(d+x) = mg + F ……②
が成り立っています。
①式を②式に代入すると、
k(d+x) = kd + F
∴ kd + kx = kd + F
∴ F = kx
となります。
（おもりをつるした状態を自然長の状態であるかのように考えて解くというのがこの手の問題のパターンです）