qGBBC　■わかりやすい高校物理の部屋■

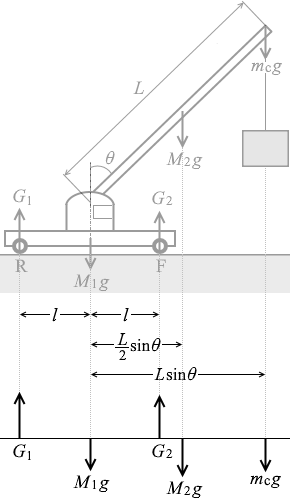
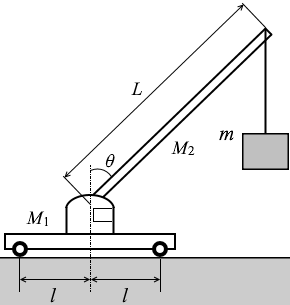
水平な地面に停めたクレーン車で、荷物をつり上げて移動させることを考える。このクレーン車は、図2のように、質量 M₁ の車体部と長さ L で質量 M₂ の一様なアーム（腕の部分）からなり、車体部はその中心から l の距離にある前後の車輪で支えられている。アームは車体部の前後方向に平行な鉛直面（図の紙面）内でのみ運動し、アームが鉛直方向となす角度 θ が変化する。ただし、θ の変化以外にクレーン車の変形はなく、ロープは質量が無視でき摩擦なく動くものとする。また、上端からロープでつる荷物の質量を m とし、重力加速度の大きさを g とする。

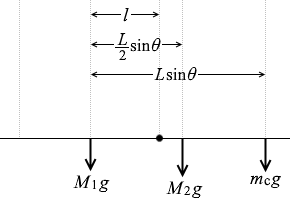
（問4）静止したクレーン車には、図3のように、重力 M₁g 、M₂g 、ロープから受ける張力 mg 以外に、後輪Rと前輪Fを通して地面から大きさ G₁ と G₂ の垂直抗力がはたらく。これらの力が満たすつり合いの式を求めよ。

（問5）荷物の質量 m がある値 m_c を超えると、後輪Rが浮いて、クレーン車が転倒することがわかった。m = m_c では、後輪Rを通してはたらく垂直抗力 G₁ は 0 になる。このときの前輪Fのまわりの力のモーメントのつり合いの式を求めよ。

（問6）qGBBD

（問7）qGBBE

#センター08本試

（問4）
問題文中で示された5つの力は向きがすべて鉛直方向になっています。斜め方向の力はありません。上向きの力の合計と下向きの力の合計が等しければつり合っていることになります。

　　　　G₁ + G₂ = M₁g + M₂g + mg

本問は『剛体にはたらく力のつり合いの条件』の①、②のうちの①についてのみを問題としています。②については以下の問5で問われます。

（問5）
各力を作用線の定理によって移動し、一直線上に並べて考えます。

題意より、G₁ = 0 であり、また、前輪Fのまわりの力のモーメントについて考えるので、G₂ については考える必要はありません。腕の長さが 0 だからです。

整理すると以下のようになります。

反時計回りの力のモーメント： M₁g × l

時計回りの力のモーメント　： M₂g × (\(\large{\frac{L}{2}}\)sinθ - l) + M_cg × (Lsinθ - l)

よって、力のモーメントのつり合いの式は

　　　　M₁gl = M₂g(\(\large{\frac{L}{2}}\)sinθ - l) + M_cg(Lsinθ - l)　　＊　M₁gl - M₂g(\(\large{\frac{L}{2}}\)sinθ - l) - M_cg(Lsinθ - l) = 0　
と表現してもいいです。閉じる