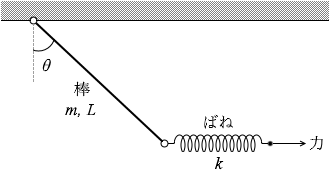
長さ L 、質量 m の一様な棒の一端を天井に取り付け、他端にばね定数 k のばねをつないだ。ある力でばねを横に引くと、図5のように棒と鉛直方向とのなす角が θ となり、ばねは水平になって静止した。このとき、ばねは自然の長さからどれだけ伸びているか。ただし、天井と棒、棒とばねは自由に回転できるようにつながれており、棒とばねは鉛直面内にあるとする。また、ばねの質量は無視できるものとし、重力加速度の大きさを g とする。
#センター11本試
長さ L 、質量 m の一様な棒の一端を天井に取り付け、他端にばね定数 k のばねをつないだ。ある力でばねを横に引くと、図5のように棒と鉛直方向とのなす角が θ となり、ばねは水平になって静止した。このとき、ばねは自然の長さからどれだけ伸びているか。ただし、天井と棒、棒とばねは自由に回転できるようにつながれており、棒とばねは鉛直面内にあるとする。また、ばねの質量は無視できるものとし、重力加速度の大きさを g とする。
#センター11本試
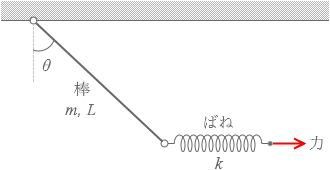求めるばねの伸びを x と置きますと、ばねを引く力の大きさは kx です。
この力は
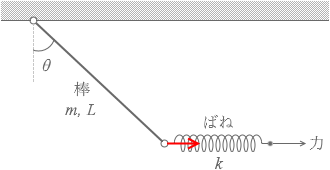棒の下端を横に引く力でもあります。
このことは初学者の方は忘れがちです。
x だけ伸びたとき、
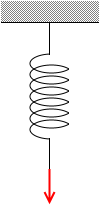引っ張る力の大きさは
kx でありますが、
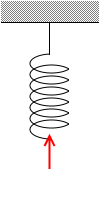この力で、
引っ張り上げていますし、
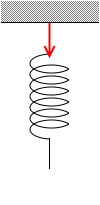この力で、
引っ張り下げていますし、
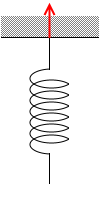この力で、
引っ張り上げています。
作用反作用の法則です。
『張力』項もご参照ください。
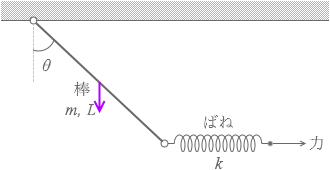一方、棒に掛かる重力の大きさは mg であり、一様な棒の重心はその中点にあります。
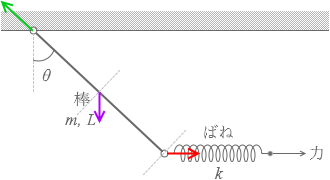とうわけで、棒に掛かる力は左図の3つです。
そして、棒が回転せずに静止しているということはこれらの力のモーメントの和が 0 ということでありますから、棒と天井の接点を中心とする力のモーメントのつり合いの式を立てますと、
0 - mg×\(\large{\frac{L}{2}}\)sinθ + kx×Lcosθ = 0 （左回りを正。『qG931』『qG6Q1』参照）
∴ kx×Lcosθ = mg×\(\large{\frac{L}{2}}\)sinθ
∴ kxcosθ = mg×\(\large{\frac{1}{2}}\)sinθ
∴ x = \(\large{\frac{mg\sinθ}{2k\cosθ}}\)
∴ x = \(\large{\frac{mg\tanθ}{2k}}\)