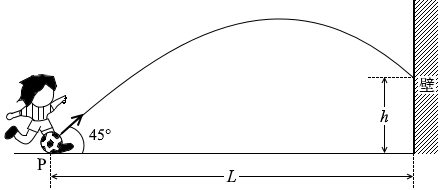
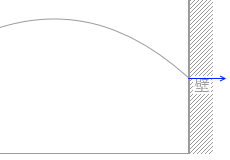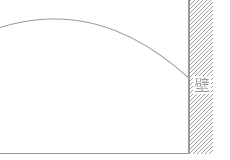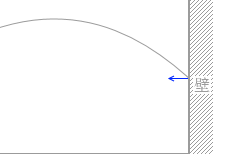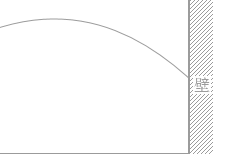
図1のように、壁から水平に距離 L だけ離れた点Pから、水平からの角度45°、速さ v0 の初速度でボールを蹴り上げると、ボールは最高点に達した後、直接、壁にぶつかった。ただし、ボールの大きさと空気の抵抗を無視し、ボールの質量を m 、重力加速度の大きさを g とする。
（問1）
（問2）qG7F1
（問3）ボールが壁にぶつかってはねかえったとき、壁がボールに与えた力積の大きさはいくらか。ただし、ボールと壁との間の反発係数は 0.5 で、壁はなめらかであるとする。
#センター02本試
図1のように、壁から水平に距離 L だけ離れた点Pから、水平からの角度45°、速さ v0 の初速度でボールを蹴り上げると、ボールは最高点に達した後、直接、壁にぶつかった。ただし、ボールの大きさと空気の抵抗を無視し、ボールの質量を m 、重力加速度の大きさを g とする。
（問1）
（問2）qG7F1
（問3）ボールが壁にぶつかってはねかえったとき、壁がボールに与えた力積の大きさはいくらか。ただし、ボールと壁との間の反発係数は 0.5 で、壁はなめらかであるとする。
#センター02本試
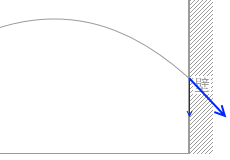「壁がなめらか」
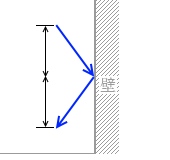なめらかな面であれば鉛直成分は変化しません。
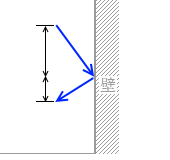あらい面ですと引っかかって小さくなります。
ということなので、速度の鉛直成分はぶつかる前とぶつかった後で変化しません。等速です。鉛直方向には力積を与えません。
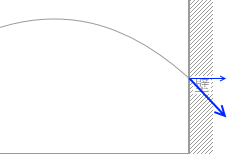考えるべき力積は水平方向成分のみです。
ぶつかる直前の水平方向の速さは、ボールを蹴った初速度の水平成分と同じであり、qG7F1より \(\large{\frac{1}{\sqrt{2}}}\)v0 です。
そして、反発係数が 0.5 であるので、ぶつかった後の速度の水平成分は 0.5×\(\large{\frac{1}{\sqrt{2}}}\)v0 です。
よって、右向きを正としますと、
ぶつかる前の運動量の水平成分 ： m (\(\large{\frac{1}{\sqrt{2}}}\)v0)
ぶつかった後の運動量の水平成分 ： m (- 0.5×\(\large{\frac{1}{\sqrt{2}}}\)v0)
であり、力積というのは（後の運動量）から（前の運動量）を引いたものだから、これを I と置くと、
I = m (- 0.5×\(\large{\frac{1}{\sqrt{2}}}\)v0) - m (\(\large{\frac{1}{\sqrt{2}}}\)v0)
∴ = (- \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{\sqrt{2}}}\)mv0) - (\(\large{\frac{1}{\sqrt{2}}}\)mv0)
∴ = - \(\large{\frac{3}{2}}\)×\(\large{\frac{1}{\sqrt{2}}}\)mv0
∴ = - \(\large{\frac{3}{2\sqrt{2}}}\)mv0
問題は大きさを聞いているので
I = \(\large{\frac{3}{2\sqrt{2}}}\)mv0
となります。
（元の運動量の 1.5倍 の力積ということです。もし反発係数が 0.6 なら 1.6倍 で、0.7 なら 1.7倍 です。）