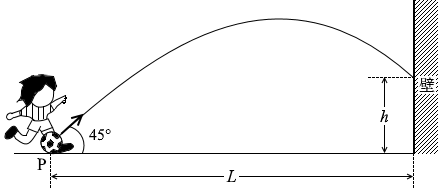
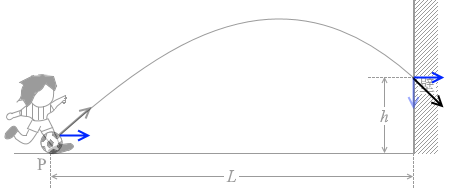
図1のように、壁から水平に距離 L だけ離れた点Pから、水平からの角度45°、速さ v0 の初速度でボールを蹴り上げると、ボールは最高点に達した後、直接、壁にぶつかった。ただし、ボールの大きさと空気の抵抗を無視し、ボールの質量を m 、重力加速度の大きさを g とする。
(問1)ボールが壁にぶつかった点の高さ h を L 、g 、v0 を用いて式で表わせ。
(問2)壁にぶつかる直前のボールの速さを v0 、g 、h を用いて式で表わせ。
(問3)qG7F2
#センター02本試
図1のように、壁から水平に距離 L だけ離れた点Pから、水平からの角度45°、速さ v0 の初速度でボールを蹴り上げると、ボールは最高点に達した後、直接、壁にぶつかった。ただし、ボールの大きさと空気の抵抗を無視し、ボールの質量を m 、重力加速度の大きさを g とする。

(問1)ボールが壁にぶつかった点の高さ h を L 、g 、v0 を用いて式で表わせ。
(問2)壁にぶつかる直前のボールの速さを v0 、g 、h を用いて式で表わせ。
(問3)qG7F2
#センター02本試
(問1)ボールが壁にぶつかった点の高さ h を L 、g 、v0 を用いて式で表わせ。
『斜方投射を表す式』を理解していれば簡単な問題です。水平成分と鉛直成分に分解して考えます。
 初速度の水平成分は
初速度の水平成分は
v0cos45° = \(\large{\frac{1}{\sqrt{2}}}\)v0 『斜方投射を表す式』の速度 vx = v0cosθ のことです。
であり、
 この水平成分が L だけ進むのに掛かる時間を t と置きますと、
この水平成分が L だけ進むのに掛かる時間を t と置きますと、
t = \(\large{\frac{距離}{速さ}}\) = \(\large{\frac{L}{\frac{1}{\sqrt{2}}v_0}}\) = \(\sqrt{2}\large{\frac{L}{v_0}}\)
つまり、壁に衝突するまでの時間は t = \(\sqrt{2}\large{\frac{L}{v_0}}\) です。
 初速度の鉛直成分は
初速度の鉛直成分は
v0sin45° = \(\large{\frac{1}{\sqrt{2}}}\)v0
であり、
この鉛直成分は鉛直上方投射運動をすると考えられ、t = \(\sqrt{2}\large{\frac{L}{v_0}}\) だけ時間が経ったときの高さは
h = \(\large{\frac{1}{\sqrt{2}}}\)v0t - \(\large{\frac{1}{2}}\)gt2 『斜方投射を表す式』の位置 y = v0sinθ⋅t - \(\large{\frac{1}{2}}\)gt2 のことです。
= \(\large{\frac{1}{\sqrt{2}}}\)v0⋅\(\sqrt{2}\large{\frac{L}{v_0}}\) - \(\large{\frac{1}{2}}\)g\(\big(\sqrt{2}\large{\frac{L}{v_0}}\big)\)2
= L - \(\large{\frac{gL^2}{v_0^2}}\)
です。
(問2)壁にぶつかる直前のボールの速さを v0 、g 、h を用いて式で表わせ。
求める速さを v と置き、その水平成分を vx 、鉛直成分を vy とします。
(水平成分 vx は)
 初速度の水平成分と変わらないから、
初速度の水平成分と変わらないから、
vx = \(\large{\frac{1}{\sqrt{2}}}\)v0 ……①
(鉛直成分 vy は)
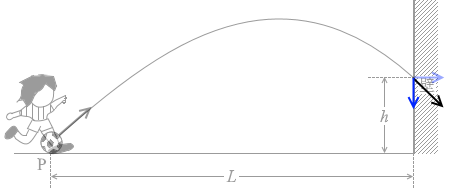 『鉛直上方投射』の t を含まない式( v2 - v02 = -2gy )を立てますと、
『鉛直上方投射』の t を含まない式( v2 - v02 = -2gy )を立てますと、
vy2 - \(\big(\large{\frac{1}{\sqrt{2}}}v_0\big)\)2 = -2gh
∴ vy2 = \(\big(\large{\frac{1}{\sqrt{2}}}v_0\big)\)2 -2gh ……②
(よって、v の大きさは)
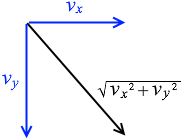 三平方の定理より、
三平方の定理より、
v = \(\sqrt{{v_x}^2+{v_y}^2}\) ①、②を代入して
∴ = \(\sqrt{(\frac{1}{\sqrt{2}}v_0)^2+(\frac{1}{\sqrt{2}}v_0)^2-2gh}\)
∴ = \(\sqrt{\frac{1}{2}{v_0}^2+\frac{1}{2}{v_0}^2-2gh}\)
∴ = \(\sqrt{{v_0}^2-2gh}\)
(別解:力学的エネルギー保存の法則を使って求めた方が、水平成分、鉛直成分に分解する必要がなくて楽)
点Pでボールを蹴った瞬間の力学的エネルギーは \(\large{\frac{1}{2}}\)mv02 (位置エネルギーは 0 ) ……③
壁にぶつかる直前の力学的エネルギーは \(\large{\frac{1}{2}}\)mv2 + mgh ……④
力学的エネルギー保存の法則により ③ = ④ であるから、
\(\large{\frac{1}{2}}\)mv02 = \(\large{\frac{1}{2}}\)mv2 + mgh
∴ mv02 = mv2 + 2mgh
∴ v02 = v2 + 2gh
∴ v2 = v02 - 2gh
∴ v = \(\sqrt{{v_0}^2-2gh}\)
と、同じ結果が楽に求められます。