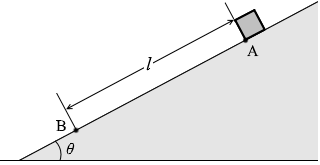
図5のような水平面と角 θ をなすなめらかな斜面がある。斜面上の点Aで、静かに小物体を離す。点Aから距離 l だけ離れた斜面上の点Bに達するまでの時間 t はいくらか。ただし、重力加速度の大きさを g とする。
#センター06追試
図5のような水平面と角 θ をなすなめらかな斜面がある。斜面上の点Aで、静かに小物体を離す。点Aから距離 l だけ離れた斜面上の点Bに達するまでの時間 t はいくらか。ただし、重力加速度の大きさを g とする。

#センター06追試
(運動方向の加速度を求める)
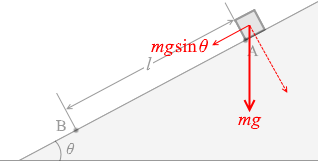 小物体の質量を m としますと、小物体には mg の重力がはたらいています。その運動方向の成分は mgsinθ です。
小物体の質量を m としますと、小物体には mg の重力がはたらいています。その運動方向の成分は mgsinθ です。
小物体の加速度を a として運動方程式を立てますと、
ma = mgsinθ
となり、計算しますと、a = gsinθ です。
これはつまり重力が sinθ 倍に小さくなったとみなすことができます。
この加速度を等加速度直線運動の変位の式 x = v0t + \(\large{\frac{1}{2}}\)at2 に当てはめますと
(あるいは自由落下運動の変位の式 y = \(\large{\frac{1}{2}}\)gt2 の g のところを gsinθ として)、
l = 0⋅t + \(\large{\frac{1}{2}}\)gsinθt2
∴ \(\large{\frac{2l}{g\sinθ}}\) = t2
∴ t = \(\large{\sqrt{\frac{2l}{g\sinθ}}}\)
となります。
(余談:もし点Bでの速さを求める問題だったら)
等加速度直線運動の v = v0 + at か、自由落下運動の v = gt に当てはめるつもりで、
a = gsinθ に t = \(\large{\sqrt{\frac{2l}{g\sinθ}}}\) を掛けて、
v = gsinθ\(\large{\sqrt{\frac{2l}{g\sinθ}}}\)
= \(\sqrt{(g\sinθ)^2\large{\frac{2l}{g\sinθ}}}\)
= \(\sqrt{2gl\sinθ}\)
と求めます。
あるいは以下のような力学的エネルギー保存の法則の式を立てて求めます。
(点Aでの位置エネルギー)+(点Aでの運動エネルギー) = (点Bでの位置エネルギー)+(点Bでの運動エネルギー)
⇔ (mglsinθ) + ( 0 ) = ( 0 ) + (\(\large{\frac{1}{2}}\)mv2)
∴ mglsinθ = \(\large{\frac{1}{2}}\)mv2
∴ glsinθ = \(\large{\frac{1}{2}}\)v2
∴ v = \(\sqrt{2gl\sinθ}\)