□
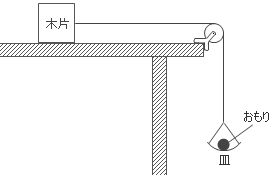
A 図1のように、水平な台の上に質量 M の木片を置き、台の端に取り付けた滑車を通して、伸び縮みしないひもで皿と結び、皿の上に質量 m のおもりをのせる。ただし、重量加速度の大きさを g とし、また、ひもと皿の質量は無視でき、滑車は軽くてなめらかに回転できるものとする。
図 1
(問1)qGCG1
B 実際には、木片と台の間には摩擦がある。静止摩擦係数 μ と動摩擦係数 μ' を求めるため、おもりの質量 m をいろいろと変えて木片の運動を調べ、次の結果を得た。
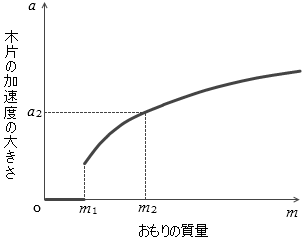
(1) m ≦ m 1 では、木片は運動しなかった。m > m 1 では、木片は等加速度で運動した。m と加速度の大きさ a の関係をクラフにすると、図2のようになった。
図 2
(問3)この結果から得られる木片と台の間の静止摩擦係数 μ の値はいくらか。
(問4)木片が運動しているとき、ひもが木片を引く力の大きさを T とすると、木片の運動方程式はどのようになるか。
(問5)図2のように m = m 2 のとき、加速度の大きさは a 2 であった。これから求められる動摩擦係数 μ' はいくらか。
(問6)さらに、おもりの質量 m を大きくしていくと、加速度の大きさ a は、ある値に近づく。その値はいくらか。
#センター01本試
(問3)
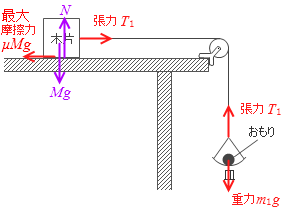
木片が台から受ける垂直抗力 を N としますと、
N = Mg
また、グラフから読み取れるのは、おもりの質量 m が 0 のときは木片はまったく動かず、m をだんだん重いものに変えていって m 1 にしたときに突然動き出した、ということです。加速度 a が 0 というのは動かないということで、m 1 のところで加速度が急に跳ね上がっているのは、突然に動き出したということです。
動き出すかどうかぎりぎりのときの張力を T 1 としますと、
T 1 = m 1 g
このときの摩擦力 (最大静止摩擦力)は
μN = μMg
動き出すかどうかぎりぎりのときというのは張力と摩擦力が同じ大きさになっているから、
T 1 = μN
⇔ m 1 g = μMg
∴ μ = \(\large{\frac{m_1}{M}}\)
(余談)斜面の縦横比 から静止摩擦係数が求められることと似ています。
(問4)木片が運動しているとき、ひもが木片を引く力の大きさを T とすると、木片の運動方程式はどのようになるか。
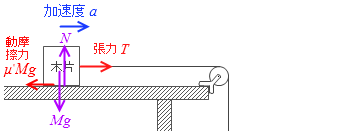
動摩擦力 は
μ'N = μ'Mg
木片の加速度の向きと張力の向きが同じで、動摩擦力の向きが反対であることに気を付けて木片の運動方程式を立てると、
Ma = T - μ'Mg
(問5)図2のように m = m 2 のとき、加速度の大きさは a 2 であった。これから求められる動摩擦係数 μ' はいくらか。
問4で求めた Ma = T - μ'Mg という式は木片が動くときの一般的な式です。a というのは変数で、いろいろな値をとります。本問はそのうちの a 2 という特定の値をとる場合の話です。
すなわち加速度が a 2 のときの木片の運動方程式は、問4で求めた式に a 2 を代入して、
Ma 2 = T - μ'Mg
一方おもりについての運動方程式は
m 2 a 2 = m 2 g - T (qGCG1 の問1の②式と同じ式です)
この2式の両辺を足し合わせて T を消去しますと、
Ma 2 + m 2 a 2 = T - μ'Mg + m 2 g - T
∴ (M + m 2 )a 2 = - μ'Mg + m 2 g
∴ μ'Mg = m 2 g - (M + m 2 )a 2
∴ μ' = \(\large{\frac{m_2g-(M+m_2)a_2}{Mg}}\)
(余談)a 2 が含まれています。動摩擦係数を求めるには M や m だけでなく a も測定しなければならないということです。また、『動摩擦力 』において、速度が変化しても動摩擦力は変化しないと説明しましたが、この場合の動摩擦力も変化しません。
(問6)さらに、おもりの質量 m を大きくしていくと、加速度の大きさ a は、ある値に近づく。その値はいくらか。
問5では m 2 、a 2 という特定の値についての運動方程式を立てましたが、本問では任意の値についての運動方程式を立てます。
まず木片については、(問4より)
Ma = T - μ'Mg
おもりについては、
ma = mg - T
2式の両辺を足し合わせて T を消去し、(問5では μ' を求めましたが)、a を求めます。
Ma + m a = T - μ'Mg + mg - T
∴ (M + m )a = (- μ'M + m )g
∴ a = \(\large{\frac{-μ'M+m}{M+m}}\)g
これが何に近づいていくのか予測するため 1 + \(\large{\frac{△}{○}}\) の形を作ります。分母分子を m で割ります。
a = \(\large{\frac{-\frac{μ'M}{m}+1}{\frac{M}{m}+1}}\)g
m を大きくしていくと \(\large{\frac{M}{m}}\) が 0 に近づいていき、上式は
a = \(\large{\frac{-0+1}{0+1}}\)g = g
に近づいていきます。
答えは g です。
これはどういうことかというと、
m が大きくなっていくと a が g に近づいていくということです。
おもりをだんだん重いものに載せ替えていくと加速度は重力加速度に近づいていき、それを超えることはないということです。木片 M がとても軽くて、おもり m がとても重かったりすれば、摩擦の影響はほとんど無くなり、重力にまかせて落下していくという考えてみれば当たり前のことです。
↑
↓
 このときの
このときの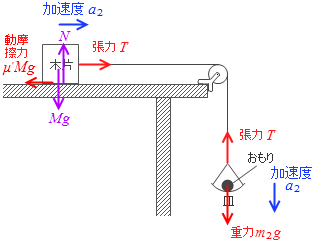
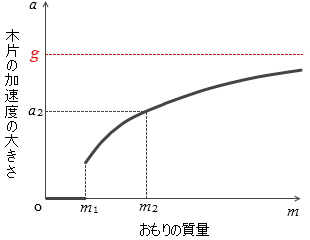 問題文のグラフにおいて m が大きくなっていくと a が g に近づいていくということです。
問題文のグラフにおいて m が大きくなっていくと a が g に近づいていくということです。