摩擦角

傾きを徐々に大きくしていく

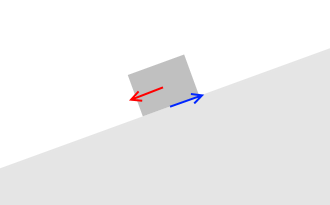
あらい斜面の上に物体を置き、斜面の傾きを徐々に大きくしていくと、ある特定の角度のところで物体が滑り落ちます。

この角度は、実は物体の質量に無関係です。斜面と物体との静止摩擦係数のみで決まります。

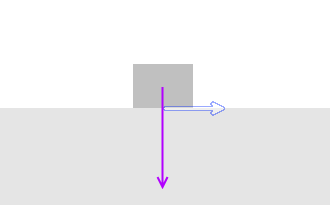
滑り落ちない状態というのは、滑り落とそうとする力（斜面と平行な外力）と静止摩擦力がつり合っているから落ちないわけですが、

滑り落ちるか滑り落ちないかギリギリの瞬間というのは、静止摩擦力が最大静止摩擦力に達した、というときです。外力＝静止摩擦力＝最大静止摩擦力 になったときです。このギリギリの瞬間の角度を摩擦角といいます。

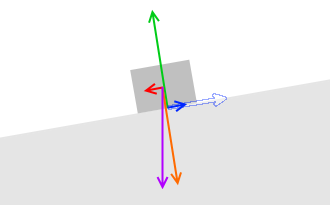
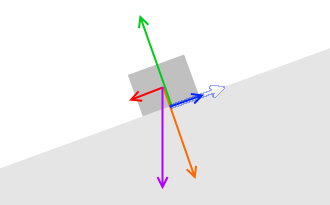
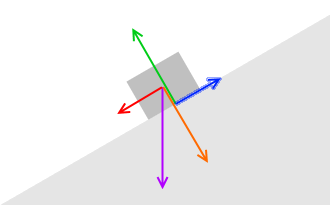
＊ アニメーションの全コマを詳しく描き出してみます。
重力の大きさはずっと一定です。
外力と静止摩擦力は少しずつ大きくなっていきます。
押し付ける力と垂直抗力と最大静止摩擦力は少しずつ小さくなっていきます。








　 閉じる

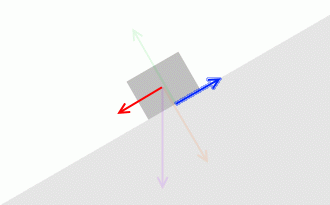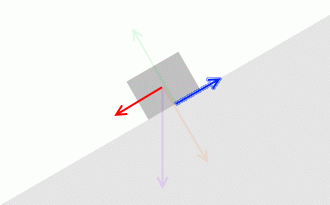この角度を上回ると、外力が最大静止摩擦力より大きくなり、物体は動き出します。

＊ 山切りモデルで説明しますと、滑り落ちるかどうかのギリギリの状態というのは、微小な山切りの斜面が水平になった状態です。
これ以上傾くと物体は滑り落ちます。
　 閉じる

摩擦角

摩擦角を θ 、静止摩擦係数を μ として、これが他の物理量を使ってどのように表されるか考えてみます。

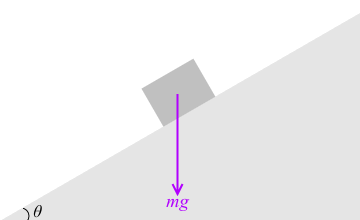物体には mg という重力がはたらいています。

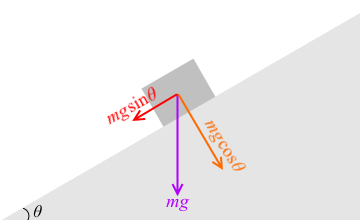その力を物体の運動方向と運動と垂直な方向に分解したときの、

物体の運動方向の力が実際に物体を滑り落とそうとする力です。sin を使って表すと、それは mgsinθ です。

運動と垂直な方向の力というのは斜面に押し付ける力です。cos を使って表すと、それは mgcosθ です。

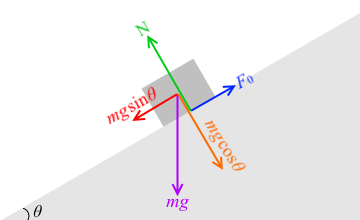いま、最大静止摩擦力 F₀ の大きさと、滑り落とそうとする力の大きさが等しいので、
　　F₀ = mgsinθ

また、垂直抗力 N の大きさと、斜面に押し付ける力の大きさは等しいので、
　　N = mgcosθ

これらを最大静止摩擦力の式に代入しますと、

　　　　F₀ = μN

　∴　　mgsinθ = μ mgcosθ

　∴　　μ = \(\large{\frac{mg\sinθ}{mg\cosθ}}\)　　　（ mgが消えます。静止摩擦係数は質量に無関係となります！）

　∴　　μ = \(\large{\frac{\sinθ}{\cosθ}}\)　　　（ \(\large{\frac{\sinθ}{\cosθ}}\)=tanθ ）

　∴　　μ = tanθ

となり、結局、摩擦角 θ は静止摩擦係数 μ のみで表されることがわかります。

ちなみに、μ = 1.0 のときというのは、摩擦角は 45° となり、また、接触面が水平であるときには、垂直抗力と最大静止摩擦力がちょうど同じ大きさになります。

＊ 問題編 qGCG2 の問3もご参照ください。斜面の話ではないのですが、静止摩擦係数 μ が単純な形で示される例を挙げています。 閉じる

相似

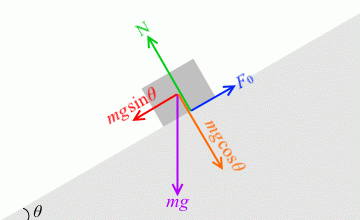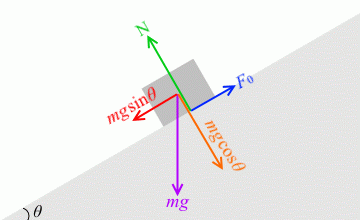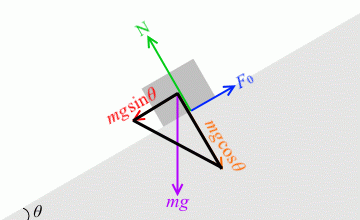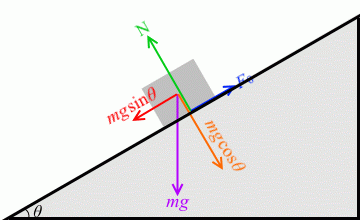摩擦角 θ と静止摩擦係数 μ の関係が μ = tanθ という単純な式で表されるのは、左図の３つの黒い三角形が相似であるからです。

たとえば、摩擦係数が 0.7 であるとき、それらの三角形の辺の比は 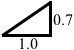となっています。tanθ = 0.7 です。摩擦係数が 0.7 ということは、たとえば垂直抗力が 1.0N のときに摩擦力が 0.7N ということです。