(問1)
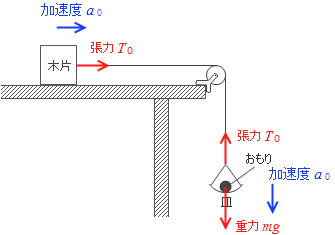
木片とおもりはひもでつながれていて、かつ木片の速さがおもりの速さを追い抜くようなことはないので、木片とおもりは一緒に動きます。このときの加速度を a0 とします。また、張力の大きさはどの地点でも一緒です。このときの張力を T0 とします。
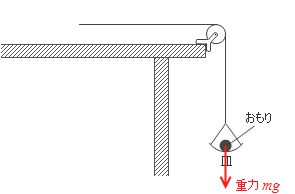 もし、木片が無ければ運動方程式は
もし、木片が無ければ運動方程式は
ma = mg
となりますが、木片がある場合はそう単純ではありません。
まず、木片だけについての運動方程式を立てますと、
Ma0 = T0 ……①
次に、おもりだけについての運動方程式を立てますと、
ma0 = mg - T0 ……②
①式を②式に代入しますと、
ma0 = mg - Ma0
∴ (M + m)a0 = mg
∴ a0 = \(\large{\frac{m}{M+m}}\)g
(問2)
上で求めた a0 を①式に代入して T0 を求めますと、
T0 = Ma0 = M\(\large{\frac{m}{M+m}}\)g = \(\large{\frac{Mm}{M+m}}\)g
(余談:1)
a0 = \(\large{\frac{m}{M+m}}\)g という式を吟味してみますと、
木片の質量 M が 0 のときは加速度が a0 = g 、つまりおもりがストンと落ちていきます。おもりの質量 m が 0 のときは加速度が a0 = 0 、つまり動きません。
T0 = \(\large{\frac{Mm}{M+m}}\)g という式を吟味してみますと、
M が 0 のときは張力が T0 = 0 、つまりおもりがストンと何の抵抗もなく落ちていきます。m = 0 のときも張力は T = 0 で、これはひもが引っ張られずブランとしている状態です。
さらに T0 = \(\large{\frac{m}{1+\frac{m}{M}}}\)g と変形して M がとても大きいときを考えてみますと、\(\large{\frac{m}{M}}\) は 0 に近づき、T0 = \(\large{\frac{m}{1+0}}\)g = mg になっていきます。ひもが杭に固定されてるかのような状態です。
(余談:2)
問1において、慣れてる人はいきなり
(M + m)a0 = mg
と立式しても構いません。運動方程式 ma = F において、m の部分が M + m で、F の部分が mg と考えるのです。加速度が発生するのは2つの物体であるが、重力がはたらくのは片方だけ、と考えます。(もちろん木片にも重力がはたらきますが、いま考えている運動(水平方向の運動)には無関係です。
この問題は『糸でつながれた物体』項で紹介したアトウッドの器械に似ています。アトウッドの器械において左側のおもりに重力がはたらかないとした場合がこの問題です。
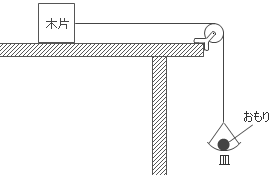

 もし、木片が無ければ
もし、木片が無ければ