なめらかに回転する軽い滑車に、軽くて伸びないひもを使って、同じ質量をもつ3個の物体を取り付けた。重力加速度の大きさを \(g\) とする。
(問3)図2のように、3個の物体A、B、Cを静止させた。物体の質量はいずれも \(m\) である。このとき、物体Aを鉛直下向きに引くひもの張力の大きさ \(T\) はいくらか。
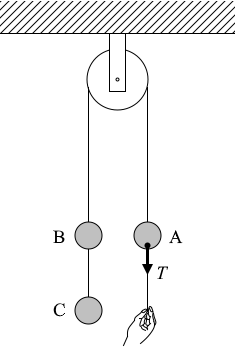
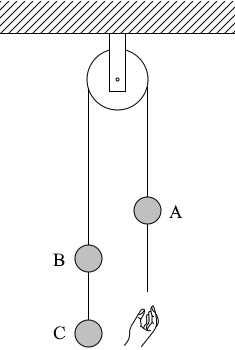
(問4)次に、図3のように、物体Aの下部のひもを静かに放して物体を運動させた。物体Aの加速度の大きさ \(a\) はいくらか。
#センター18本試物理基礎
なめらかに回転する軽い滑車に、軽くて伸びないひもを使って、同じ質量をもつ3個の物体を取り付けた。重力加速度の大きさを \(g\) とする。
(問3)図2のように、3個の物体A、B、Cを静止させた。物体の質量はいずれも \(m\) である。このとき、物体Aを鉛直下向きに引くひもの張力の大きさ \(T\) はいくらか。

(問4)次に、図3のように、物体Aの下部のひもを静かに放して物体を運動させた。物体Aの加速度の大きさ \(a\) はいくらか。

#センター18本試物理基礎
(問3)
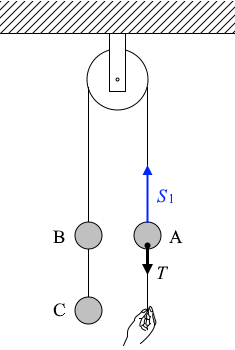 物体Aを持ち上げる張力を \(\color{blue}S_1\) とおきますと、
物体Aを持ち上げる張力を \(\color{blue}S_1\) とおきますと、
ひとつながりのひもの張力の大きさはどこもかしこも同じなので
 物体Aと物体Bをつなぐひもにはたらく張力の様子は左図のようになります。
物体Aと物体Bをつなぐひもにはたらく張力の様子は左図のようになります。
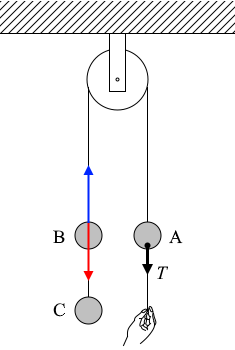 いま各物体は静止しており、静止しているということは力がつり合っているということであり、物体Bと物体Cを合わせた重さは \(\color{red}2mg\) なので、\(\color{blue}S_1\) も \(\color{blue}2mg\) ということになります。
いま各物体は静止しており、静止しているということは力がつり合っているということであり、物体Bと物体Cを合わせた重さは \(\color{red}2mg\) なので、\(\color{blue}S_1\) も \(\color{blue}2mg\) ということになります。
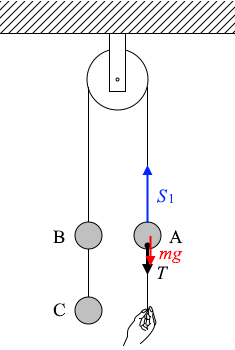 つまり物体Aを持ち上げる力は \(\color{blue}2mg\) であり、物体Aを下に引っ張る力は張力 \(T\) と物体Aの重さ \(\color{red}mg\) であるから、
つまり物体Aを持ち上げる力は \(\color{blue}2mg\) であり、物体Aを下に引っ張る力は張力 \(T\) と物体Aの重さ \(\color{red}mg\) であるから、
\({\color{blue}2mg} = T + \color{red}mg\)
∴ \(T = mg\)
(暗算で解くとすると)
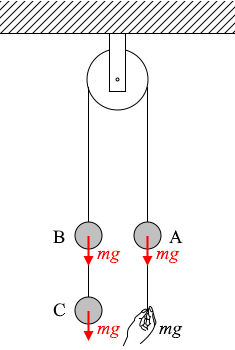 左図のような力関係なのだから手が引く力の大きさは \(mg\) のはず、となります。
左図のような力関係なのだから手が引く力の大きさは \(mg\) のはず、となります。
(問4)
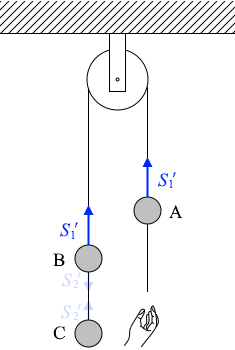 物体Aと物体Bとの間の張力を \(\color{blue}{S_1}'\) とおきます。運動しているので問3の \(\color{blue}S_1\) と同じというわけではありません。ひとつながりのひもの張力がどこもかしこも同じであることは変わりありません。
物体Aと物体Bとの間の張力を \(\color{blue}{S_1}'\) とおきます。運動しているので問3の \(\color{blue}S_1\) と同じというわけではありません。ひとつながりのひもの張力がどこもかしこも同じであることは変わりありません。
物体Bと物体Cとの間の張力は \(\color{blue}{S_2}'\) とおくことにしますが、物体Bと物体Cは一体と考え、とりあえず \(\color{blue}{S_2}'\) のことは考えません。
加速度の大きさは3物体とも同じです。ひもはたるむはずはないので3物体は同時に動き、その加速度の大きさはともに \(a\) です。
運動方程式を立てて加速度 \(a\) の大きさを求めます。
物体Aについての運動方程式は
\(ma = {\color{blue}{S_1}'} - mg\) ……①
物体Bと物体Cについての運動方程式は
\((m+m)a = mg + mg - \color{blue}{S_1}'\) ……②
上式は反時計回りを正の方向として立式したものですが、
そうではなく、鉛直上向きを正の方向とし、
物体A:\(ma = {\color{blue}{S_1}'} - mg\)
物体B、C:\((m+m)×(-a) = - \ mg - mg + \color{blue}{S_1}'\)
と立式してもいいです。同じことですが。
なお、物体Aの式を \(ma = mg - {\color{blue}{S_1}'}\) とやってしまうと正しい答えが導けなくなるのでご注意ください。
①式と②式の両辺を足し合わせますと、
\((m+m)a + ma = mg + mg - mg\) ……③
∴ \(3ma = mg\)
∴ \(a = {\large\frac{1}{3}}g\)
(\(\color{blue}{S_1}'\) を求めてみる)
上の結果を①式に代入してみますと、
\({\large\frac{1}{3}}mg = {\color{blue}{S_1}'} - mg\)
∴ \({\color{blue}{S_1}'} = {\color{blue}{\large\frac{4}{3}}mg}\)
(\(\color{blue}{S_2}'\) を使って、物体B単独、物体C単独についての式を立ててみる)
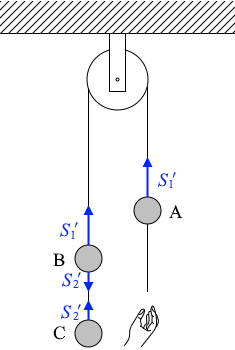 物体B単独についての運動方程式は
物体B単独についての運動方程式は
\(ma = mg + {\color{blue}{S_2}'} - {\color{blue}{S_1}'}\) ……④
物体C単独についての運動方程式は
\(ma = mg - {\color{blue}{S_2}'}\) ……⑤
\(a = {\large\frac{1}{3}}g\) を⑤式に代入しますと、
\({\large\frac{1}{3}}mg = mg - {\color{blue}{S_2}'}\)
∴ \({\color{blue}{S_2}'} = {\color{blue}{\large\frac{2}{3}}mg}\)
\(a\)、\(\color{blue}{S_1}'\)、\(\color{blue}{S_2}'\) の値を④式に代入しますと、
\({\large\frac{1}{3}}mg = mg + {\large\frac{2}{3}}mg - {\large\frac{4}{3}}mg\)
となり、矛盾がないことがわかります。
(問3では言及しませんでしたが \(\color{blue}S_2\) の大きさは)
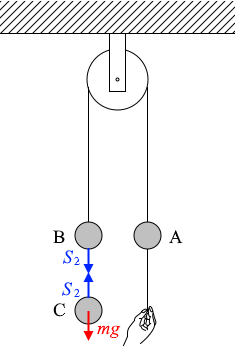 物体Cがぶら下がっているだけなので \(\color{blue}mg\) です。
物体Cがぶら下がっているだけなので \(\color{blue}mg\) です。
つまり
\({\color{blue}S_1} = {\color{blue}2mg}\)
\({\color{blue}S_2} = {\color{blue}mg}\)
だったものが、手を離したとたん
\({\color{blue}{S_1}'} = {\color{blue}{\large\frac{4}{3}}mg}\)
\({\color{blue}{S_2}'} = {\color{blue}{\large\frac{2}{3}}mg}\)
になったということです。
(問4を暗算で解くとすると)
水平方向の運動に変換して考え、

運動方程式を立てますと、
\((m+m+m)a = mg + mg - mg\)
∴ \(a = {\large\frac{1}{3}}g\)
と求まりますが、よく見ますと、これは上の③式そのものとなってます。加速度を求めるには③式だけ立てればいいということです。
たとえば他に、左向きが3個、右向きが1個だったりする場合は
\((m+m+m+m)a = mg + mg + mg - mg\)
∴ \(a = {\large\frac{2}{4}}g\)
と求まり、左向きが3個、右向きが2個だったりする場合は
\((m+m+m+m+m)a = mg + mg + mg - mg - mg\)
∴ \(a = {\large\frac{1}{5}}g\)
と求まります。
そしてこれは『糸でつながれた物体』項の『運動方程式を立てる』の
\({\color{#0b0}a = ({\large\frac{M-m}{M+m}})g}\)
のことです。