自然の長さ l 、ばね定数 k の二つの軽いばねを、質量 m の小球の上下に取り付けた。下側のばねの端を床に取り付け、上側のばねの端を手で引き上げた。重力加速度の大きさを g とする。
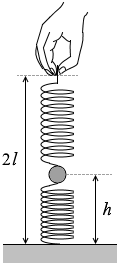
（問3）図2のように、ばねの長さの合計を 2l にして小球を静止させた。小球の床からの高さ h を式で表わせ。ただし、二つのばねと小球は同一鉛直線上にあるものとする。
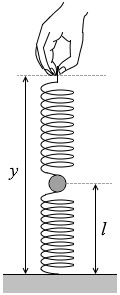
（問4）次に、図3のように、床から測った小球の高さが l になるまで、ばねの上端をゆっくり引き上げた。このときのばねの長さの合計 y と、高さ h から l まで小球を引き上げる間に手がした仕事 W を表す式の組合せとして正しいものを、下の①～⑥のうちから一つ選べ。
| y | W | |
|---|---|---|
| ① | \(\large{\frac{mg}{2k}}\) + 2l | mg(l - h) + \(\large{\frac{k}{2}}\)(y - l)2 - k(2l - h)2 |
| ② | \(\large{\frac{mg}{2k}}\) + 2l | mg(l - h) + k(y - 2l)2 - k(l - h)2 |
| ③ | \(\large{\frac{mg}{2k}}\) + 2l | mg(l - h) + \(\large{\frac{k}{2}}\)(y - 2l)2 - k(l - h)2 |
| ④ | \(\large{\frac{mg}{k}}\) + 2l | mg(l - h) + \(\large{\frac{k}{2}}\)(y - l)2 - k(2l - h)2 |
| ⑤ | \(\large{\frac{mg}{k}}\) + 2l | mg(l - h) + k(y - 2l)2 - k(l - h)2 |
| ⑥ | \(\large{\frac{mg}{k}}\) + 2l | mg(l - h) + \(\large{\frac{k}{2}}\)(y - 2l)2 - k(l - h)2 |
#センター15本試物理Ⅰ #センター15本試物理
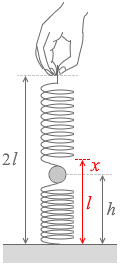l と h の差を x と置きますと、この x というのは、上側のばねの伸び幅のことであり、かつ、下側のばねの縮み幅ということになります。
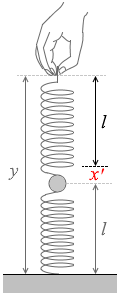下側のばねは自然長であるので力を発揮していません。小球を上に上げようとしているのは上側のばねだけであり、ばねの伸びを x' とすると x' = y - 2l であり、ばねの力と重力とのつり合いの式を立てますと、