図1のように、ばね定数 k 、自然の長さ l のばねの両端を引いたところ、自然の長さからの伸びが x になり、両端に加えた力の大きさは F になった。
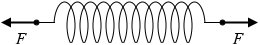
(問1)伸び x を式で表わせ。
(問2)ばねを伸ばすときに、両端に加えた力のした仕事は合わせていくらになるか。
#センター15本試物理基礎
図1のように、ばね定数 k 、自然の長さ l のばねの両端を引いたところ、自然の長さからの伸びが x になり、両端に加えた力の大きさは F になった。
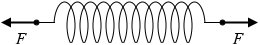
(問1)伸び x を式で表わせ。
(問2)ばねを伸ばすときに、両端に加えた力のした仕事は合わせていくらになるか。
#センター15本試物理基礎
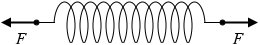 この状況というのは
この状況というのは
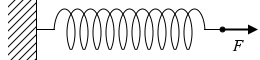 この状況とまったく同じです。
この状況とまったく同じです。
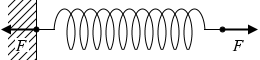 『作用⋅反作用の法則』項で説明したように、壁には左向きの力が隠されています。
『作用⋅反作用の法則』項で説明したように、壁には左向きの力が隠されています。
(『qI7H2』参照)
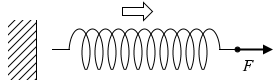 もし左向きの力が隠れていないとすれば、ばねは右に移動していってしまいます。
もし左向きの力が隠れていないとすれば、ばねは右に移動していってしまいます。
というわけで、
 このような状況であると考えて普通に解くと、
このような状況であると考えて普通に解くと、
(問1)
フックの法則より、
F = kx
∴ x = \(\large{\frac{F}{k}}\)
(問2)
力のした仕事(= 弾性力による位置エネルギー)は
\(\large{\frac{kx^2}{2}}\)
(良問)
この問題は作用⋅反作用の法則をちゃんと理解しているかを問う非常にいい問題です。
(間違いやすい考え方)
この問題を
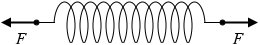 2F = kx
2F = kx
と考えてしまうのは間違いです。作用⋅反作用の法則に反します。力は対になって1つの力です。
あるいは、
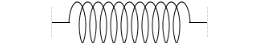
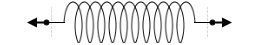
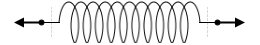
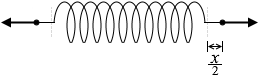 片側だけに着目して
片側だけに着目して
F = k\(\large{\frac{x}{2}}\)
などと考えるのも間違いです。問題文に「伸びが x になり、両端に加えた力の大きさは F になった」と書いてあります。半分の伸びでフルマックスの F の力を発揮しているのはおかしいです。