物体Bが滑り落ちるかどうかはμ が大きければ滑り落ちにくいですし、小さければ滑り落ちやすいです。θ が大きければ滑り落ちやすいですし、小さければ滑り落ちにくいです。F が大きければ滑り落ちやすいですし、小さければ滑り落ちにくいです。
(問1)μ がいくら以上であれば滑り落ちないか考えます。摩擦角 を求める話とほぼ一緒です*
『摩擦角』項は静止摩擦係数が固定されていて斜面の角度が変化するというようなイメージ、閉じる
mg
この重力を運動方向とそれに垂直な方向に分解しますと、
mg sinθ mg cosθ
mg cosθ mg cosθ
mg sinθ mg sinθ
μ であるときの最大静止摩擦力 は μ × 垂直効力 であり、μmg cosθ
この最大静止摩擦力が mg sinθ
μmg cosθ mg sinθ
∴ μ ≧ \(\large{\frac{mg\sinθ}{mg\cosθ}}\)
∴ μ ≧ tanθ
(矢印の起点はいい加減でも減点されないと思いますが、矢印の大きさと向きは、ちゃんと3つのベクトルの和が 0 になるように描かないと減点されるかもしれません。また、静止摩擦力の所を最大静止摩擦力と書いてしまうと減点されるかバツにされると思います。)
図 2
図 3
図 4
(問2)F が小さければ、物体Bが滑り落ちないこともあり得ます。上の図2のような運動です。
滑り落ちなければ台Aと物体Bは一体であるとみなすことができ、求める加速度を a とすると、以下のような運動方程式が立てられます。
(M + m )a = F
∴ a = \(\large{\frac{F}{M+m}}\)
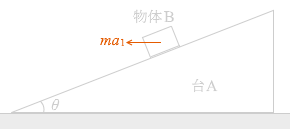
(問3)F を徐々に大きくしていくと図3のように物体Bが滑り落ちるようになります。この図2から図3への境となる力の大きさを求めよ、というのが問3の趣旨です。
ぎりぎり滑り落ちないときの力が F 1 であるとすると、このときの台Aと物体Bの加速度(a 1 と置く)は、問2と同じように考えて、
(M + m )a 1 = F 1 ……①
∴ a 1 = \(\large{\frac{F_1}{M+m}}\)
この加速度で台Aと物体Bは運動しています。
そしてこのとき、台Aと一緒に運動している観測者から物体Bを見ると、
ma 1 慣性力 がはたらいているように感じられます。
ma 1 mg
これらを、斜面方向と斜面に垂直な方向に分解しますと、
ma 1 cosθ ma 1 sinθ mg cosθ mg sinθ
mg cosθ ma 1 sinθ mg cosθ - ma 1 sinθ
μ (mg cosθ - ma 1 sinθ )
ma 1 cosθ mg sinθ
すなわち、
ma 1 cosθ mg sinθ μ (mg cosθ - ma 1 sinθ )
∴ a 1 cosθ + g sinθ = μ (g cosθ - a 1 sinθ )
∴ a 1 cosθ + μa 1 sinθ = μg cosθ - g sinθ
∴ (cosθ + μ sinθ )a 1 = (μ cosθ - sinθ )g
∴ a 1 = \(\large{\frac{μ\cosθ-\sinθ}{μ\sinθ+\cosθ}}\)g
①式 (M + m )a 1 = F 1 に代入すると、
F 1 = \(\large{\frac{μ\cosθ-\sinθ}{μ\sinθ+\cosθ}}\)(M + m )g
(問4)F が十分大きくて、F の大きさによらない運動というのはまさに図4のような状態であるということです。
台Aを引いた途端、物体Bは自由落下運動を始める。
(余談:1)F を大きくしていくと図4の状態になるわけですが、この図3と図4の境となる力の大きさ(F 2 と置きます)を求めてみます。
その境となるときというのは、垂直抗力が 0 となるときです。このときは台Aと物体Bが互いに影響を及ぼし合っていないので、F 2 の力は台Aだけに掛かり、台Aの加速度を a 2 として運動方程式を立てますと、
Ma 2 = F 2 ……②
となり、
a 2 = \(\large{\frac{F_2}{M}}\)
と加速度が求まります。
ma 2
ma 2 mg
これらを、斜面方向と斜面に垂直な方向に分解しますと、
ma 2 cosθ ma 2 sinθ mg cosθ mg sinθ
ma 2 sinθ mg cosθ
ma 2 sinθ mg cosθ
∴ a 2 sinθ = g cosθ
∴ a 2 = \(\large{\frac{\cosθ}{\sinθ}}\)g
∴ a 2 = \(\large{\frac{1}{\tanθ}}\)g
②式 Ma 2 = F 2 に代入しますと、
F 2 = \(\large{\frac{1}{\tanθ}}\)Mg
これが図3の状況から図4の状況に変わるときの境の状態です。もうここまでくると物体Bの質量 m や静止摩擦係数 μ は関係無くなります。
(余談:2)
mg sinθ ma cosθ mg sinθ - ma cosθ
もうちょっと強い力で押すと、
mg sinθ ma 3 cosθ
このときの加速度を求めますと、
mg sinθ = ma 3 cosθ
∴ g sinθ = a 3 cosθ
∴ a 3 = g tanθ
運動方程式を立てて力の大きさを求めますと、
(M + m )a 3 = F 3
∴ F 3 = tanθ (M + m )g (向きは左)
(余談:3)
物体Bが斜面を登るかどうかの境の状況では、
ma 4 cosθ mg sinθ μ (mg cosθ + ma 1 sinθ )
となっています。
∴ a 4 cosθ - g sinθ = μ (g cosθ + a 4 sinθ )
∴ a 4 cosθ - μa 4 sinθ = μg cosθ + g sinθ
∴ (cosθ - μ sinθ )a 4 = (μ cosθ + sinθ )g
∴ a 4 = \(\large{\frac{μ\cosθ+\sinθ}{-μ\sinθ+\cosθ}}\)g
運動方程式を立てて力の大きさを求めますと、
(M + m )a 4 = F 4
∴ F 4 = \(\large{\frac{μ\cosθ+\sinθ}{-μ\sinθ+\cosθ}}\)(M + m )g (向きは左)
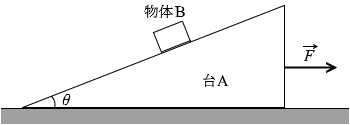
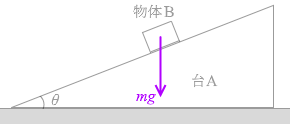 物体Bには重力
物体Bには重力 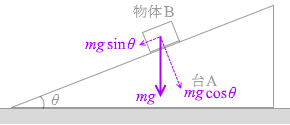 このようになります。
このようになります。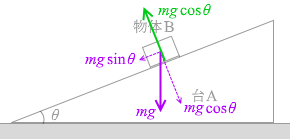 運動方向と垂直な力
運動方向と垂直な力 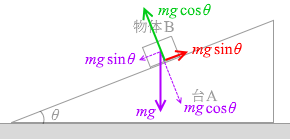 運動方向の力
運動方向の力 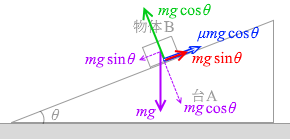 そして、静止摩擦係数が μ であるときの
そして、静止摩擦係数が μ であるときの 物体Bにはたらく力と名称は左図の3つです。これら3つの力がつり合って、物体Bは静止しています。
物体Bにはたらく力と名称は左図の3つです。これら3つの力がつり合って、物体Bは静止しています。


 物体Bには
物体Bには 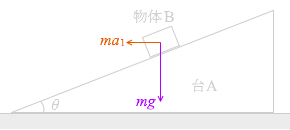 つまり、物体Bには
つまり、物体Bには 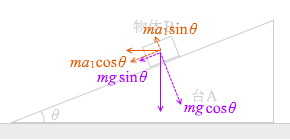 それぞれ、
それぞれ、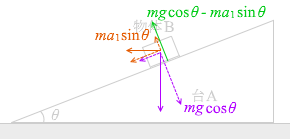 よって、垂直抗力の大きさは
よって、垂直抗力の大きさは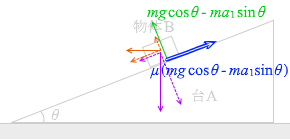 最大静止摩擦力は静止摩擦係数と垂直抗力を掛けたものだから、
最大静止摩擦力は静止摩擦係数と垂直抗力を掛けたものだから、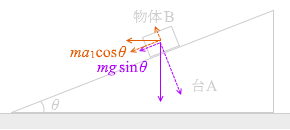 物体Bを滑り落とそうとする力は
物体Bを滑り落とそうとする力は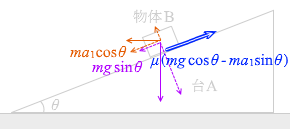 今は、この力がちょうど最大静止摩擦力と同じになっていて物体Bがぎりぎり踏み留まっています。(もし最大静止摩擦力より大きくなれば図3のように滑り落ちていきます)
今は、この力がちょうど最大静止摩擦力と同じになっていて物体Bがぎりぎり踏み留まっています。(もし最大静止摩擦力より大きくなれば図3のように滑り落ちていきます)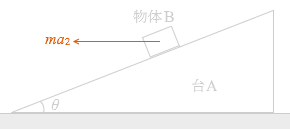 そして、台Aから見ると、物体Bには
そして、台Aから見ると、物体Bには 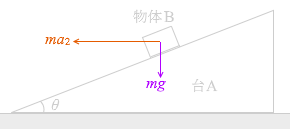 つまり、物体Bには
つまり、物体Bには 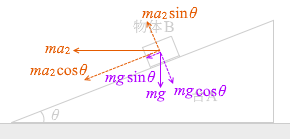 それぞれ、
それぞれ、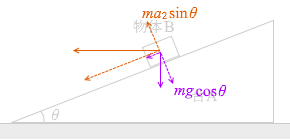 斜面に垂直な成分の
斜面に垂直な成分の 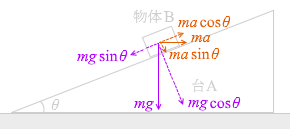 こんな感じになり、
こんな感じになり、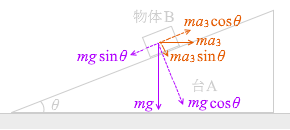
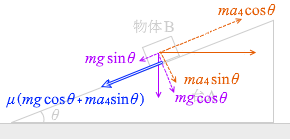 余談2の場合より強い力で押した場合は、摩擦力の向きは逆になります。上に登って行こうとする動きを阻止しようとする向きです。
余談2の場合より強い力で押した場合は、摩擦力の向きは逆になります。上に登って行こうとする動きを阻止しようとする向きです。