図2のように、水平面上に質量 m の物体を置き、壁との間をばね定数 k のばねでつないだ。ばねの自然の長さからの伸びを x で表し、面と物体の間の静止摩擦係数を μ 、動摩擦係数を μ' 、重力加速度の大きさを g とする。
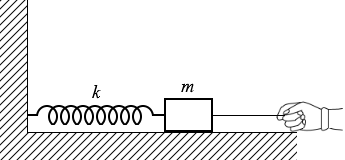 図 2
図 2
(問4)ばねが自然の長さにある状態から、図2のように手で水平に物体に力を加え、ばねを引き伸ばした。ばねの伸びが x になるまでに、手によってなされた仕事はいくらか。
(問5)問4の過程の最後に手を止めて静かに離したところ、物体は静止していた。手を離したあとも物体が静止しているようなばねの伸び x の最大値 x0 はいくらか。
(問6)問5の実験でばねの伸びが x < x0 のとき、物体に作用している摩擦力はいくらか。
#センター06本試
(問4)ばねが自然の長さにある状態から、図2のように手で水平に物体に力を加え、ばねを引き伸ばした。ばねの伸びが x になるまでに、手によってなされた仕事はいくらか。
手によってなされた仕事は2種類あります。ばねの力に逆らってした仕事と(W1と置きます)、摩擦力に逆らってした仕事です(W2と置きます)。
ばねの力に逆らってした仕事というのは弾性エネルギーのことであり、
W1 = \(\large{\frac{1}{2}}\)kx2
です。
摩擦力に逆らってした仕事というのは、摩擦力と移動距離を掛けたものです。摩擦力は動摩擦係数と垂直抗力を掛けたものです。物体には mg の重力が掛かり、これを反対向きにしたものが垂直抗力です。要するに、
W2 = (摩擦力)×(移動距離) = (動摩擦係数)×(垂直抗力)×(移動距離)= μ'×mg×x
です。
求める仕事は
W1 + W2 = \(\large{\frac{1}{2}}\)kx2 + μ'mgx
です。
(問5)問4の過程の最後に手を止めて静かに離したところ、物体は静止していた。手を離したあとも物体が静止しているようなばねの伸び x の最大値 x0 はいくらか。
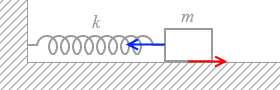 物体が静止するのは、ばねの弾性力 kx と最大静止摩擦力 μmg がつり合っているからです。
物体が静止するのは、ばねの弾性力 kx と最大静止摩擦力 μmg がつり合っているからです。
このとき μmg は固定値ですが、 kx は x によって大きくなったり小さくなったりします。ばねは大きく引っ張るほど力が大きくなります。右にいっぱい引っ張れば、手を離したときに、最大静止摩擦力を超えて左に動き出します。その動き出すかどうかのギリギリの長さを求めよ、というのが題意です。つまり、
kx ≦ μmg
ということであり、
∴ x ≦ \(\large{\frac{μmg}{k}}\)
であり、最大値は
x0 = \(\large{\frac{μmg}{k}}\)
です。
(問6)問5の実験でばねの伸びが x < x0 のとき、物体に作用している摩擦力はいくらか。
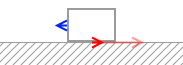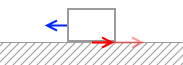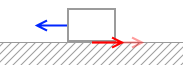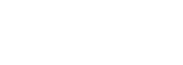 x < x0 のときというのは動かないときであり、動かないということは力がつり合っているということであり、弾性力 kx と同じ大きさの摩擦力がはたらいているということであり、つまりこのときの摩擦力の大きさは kx です。
x < x0 のときというのは動かないときであり、動かないということは力がつり合っているということであり、弾性力 kx と同じ大きさの摩擦力がはたらいているということであり、つまりこのときの摩擦力の大きさは kx です。
このときの摩擦力を『静止摩擦力』といいます。
動き出す瞬間の摩擦力は『最大静止摩擦力』といいます。
『静止摩擦力』は変動値です。弾性力の大きさに合わせて変化します。
『最大静止摩擦力』は固定値です。μmg です。弾性力が最大静止摩擦力を超えると物体は動き出します。
この辺の話はややこしいですが『静止摩擦力』をよく読んで頭を整理してください。
↑
↓

 物体が静止するのは、ばねの
物体が静止するのは、ばねの x < x0 のときというのは動かないときであり、動かないということは力がつり合っているということであり、弾性力
x < x0 のときというのは動かないときであり、動かないということは力がつり合っているということであり、弾性力