図1のように、水平な地面上の点Oから、小球1と小球2を斜め方向に同じ速さで打ち上げた。打ち上げる方向が水平面となす角度は、小球1の方が大きかった。小球1と小球2が、打ち上げられてから地面に落下するまでに要した時間をそれぞれ T1 、T2 とする。T1 と T2 の大小関係について述べた文として最も適当なものを、下の①～⑤のうちから一つ選べ。ただし、空気抵抗は無視できるものとする。
① T1 > T2 である。
② T1 < T2 である。
③ T1 = T2 である。
④ T1 とT2 の大小関係は、質量の大小関係による。
⑤ T1 とT2 に定まった大小関係はない。
#センター16本試物理
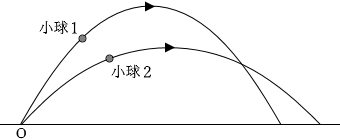
斜方投射の運動は水平方向と鉛直方向に分解することができ、落下するまでの時間は鉛直方向の運動のみによって決まり、鉛直方向の運動は鉛直上方投射の運動であり、鉛直上方投射では、（鉛直方向の）初速が大きいほど最高到達点が高く、落下するまでの時間も長いので、
答えは ① T1 > T2 である。
（数式を使って考える）
小球を打ち上げる速さを v0 、仰角を θ 、重力加速度の大きさを g とすると、斜方投射の式は以下のように表現できます。
速度 vx = v0cosθ vy = v0sinθ - gt
位置 x = v0cosθ⋅t y = v0sinθ⋅t - \(\large{\frac{1}{2}}\)gt2
軌道の式 y = tanθ⋅x - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\)x2
これらのうちの位置の式 y = v0sinθ⋅t - \(\large{\frac{1}{2}}\)gt2 に y = 0 を代入すると、
0 = v0sinθ⋅t - \(\large{\frac{1}{2}}\)gt2
∴ 0 = t(v0sinθ - \(\large{\frac{1}{2}}\)gt)
∴ t = 0 , v0sinθ - \(\large{\frac{1}{2}}\)gt = 0
∴ t = 0 , - \(\large{\frac{1}{2}}\)gt = - v0sinθ
∴ t = 0 , \(\large{\frac{2v_0\sinθ}{g}}\)
このうち地面に落下するまでに要した時間は t = \(\large{\frac{2v_0\sinθ}{g}}\) であり、
t = 0 はスタートの時間、
t = \(\large{\frac{2v_0\sinθ}{g}}\) は落下するまでの時間です。
ちなみにこれの半分の
t = \(\large{\frac{v_0\sinθ}{g}}\) は最高点に達するまでの時間です。
それぞれの仰角を θ1 、θ2 とすると、
小球1は
T1 =\(\large{\frac{2v_0\sinθ_1}{g}}\)
小球2は
T2 =\(\large{\frac{2v_0\sinθ_2}{g}}\)
そして、sinθ1 > sinθ2 であるので、
T1 > T2
落下時間を稼ぐには真上に打ち上げるのがいいということになります。ちなみに遠くに飛ばすには 45° です。