qH7D9

　図1のように、なめらかな水平面上にばねがおかれ、ばねの右端は壁に固定されている。ばねの左端に小物体をおいて、自然長からばねを長さ L だけ縮めてから、静かにはなした。その後、小物体は水平面から飛び出し、水平面の端から点Pまでのちようど半分の地点に落下した。以下の問1〜5に答えなさい。解答欄には必要に応じて導出の過程を示しなさい。なお、小物体の大きさと空気抵抗は無視できるものとする。また、文中に与えられた物理量の他に解答に必要な物理量があれば、それらを表す記号はすべて各自で定義し、解答欄に明示しなさい。

図 1

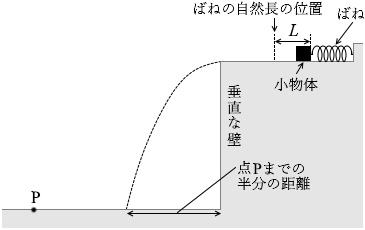
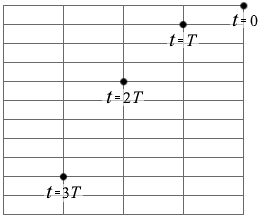
（問1）小物体が水平面から飛び出す瞬間の時刻を t = 0 としたとき、t = 0 と t = T での小物体の位置がそれぞれ黒丸で解答欄の図中に描かれている。t = 2T と t = 3T での小物体の位置を黒丸ではっきりとわかるように、それぞれ図中に描きなさい。

（問2）自然長からばねを長さ L だけ縮めてからはなしたとき、小物体がばねから離れる瞬間の速さを VL とする。小物体を点Pまで飛ばすためには、水平面から小物体が飛び出す瞬間の速さを、VL の何倍にする必要があるかを答えなさい。

（問3）小物体を点Pまで飛ばすためには、ばねを自然長からどれだけの長さ縮めてから、小物体をはなせばよいかを求めなさい。

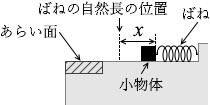
（問4）次に、図2の斜線部分 を表面のあらい水平面に置き換えた。ばねを自然長から長さ x だけ縮めてから小物体をはなしたところ、小物体は水平面から飛び出していった。このとき、小物体はあらい水平面上で等加速度運動することを説明しなさい。また、小物体がばねから離れる瞬間の速さを Vx 、小物体が水平面から飛び出す瞬間の速さを Vx' としたとき、(Vx')2 - (Vx)2 はばねを縮める長さ x によらず一定であることを説明しなさい。

図 2

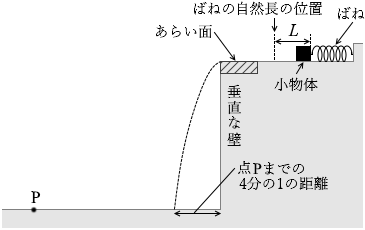
（問5）図3のように、自然長からばねを長さ L だけ縮めてからはなしたとき、小物体は水平面の端から点Pまでの \(\large{\frac{1}{4}}\) の地点に落下した。次に、ばねを自然長から長さ X だけ縮めてからはなしたところ、小物体はちようど点Pまで到達した。VL 、VL' を問4の設問で x を L として定義される速さ、VX 、VX' を問4の設間で x を X として定義される速さとする。このとき、VL' 、VX' 、VX をそれぞれ VL で表しなさい。また、\(\large{\frac{X}{L}}\) を求めなさい。

図 3

#神戸大17

（問1）
水平投射においては、水平方向は等速、鉛直方向は初速 0 の等加速度運動（時間の2乗に比例）をするから、左図のようになります。

　

　

（問2）
水平投射（x = v0t、y = \(\large{\frac{1}{2}}\)gt2）においては、高さが変わらなければ（y = \(\large{\frac{1}{2}}\)gt2 の y が不変）、落下し始めてから衝突するまでの時間は変わらないので（t 不変）、水平方向の距離（x = v0t）は初速（v0）に比例するので、その距離を2倍にするには初速を 2倍 にする必要があります。

　

　

（問3）
（VL を求めてみる）
小物体の質量を m 、ばね定数を k と置きますと、
L だけ縮めたときの力学的エネルギーは

　　　　（運動エネルギー）+（弾性エネルギー）

　　　= （ 0 ）+（ \(\large{\frac{1}{2}}\)kL2 ）　　……①

自然長になった瞬間（小物体がばねから離れる瞬間）の力学的エネルギーは

　　　　（運動エネルギー）+（弾性エネルギー）

　　　= （ \(\large{\frac{1}{2}}\)mVL2 ）+（ 0 ）　　……②

力学的エネルギー保存の法則により ① = ② であるから、

　　　　\(\large{\frac{1}{2}}\)kL2 = \(\large{\frac{1}{2}}\)mVL2

　∴　　VL2 = \(\large{\frac{k}{m}}\)L2

　∴　　VL = L\(\sqrt{\frac{k}{m}}\)

（点Pに届くには）
問2より VL を2倍にすれば点Pに届くので、そのためには L を2倍にすればよい。つまり、 2L の長さだけ縮めてからはなせばよい。

　

　

（問4）
小物体が運動する方向には動摩擦力のみがはたらき、動摩擦力の大きさは運動の速さに無関係であり、小物体に掛かる重力と動摩擦係数に比例するが、その2つが一定であるので、動摩擦力も一定であり、運動方程式の関係により加速度も一定となるので、小物体は等加速度運動を行う。

また、等加速度直線運動の公式 v2 - v02 = 2ax より、 (Vx')2 - (Vx)2 は加速度とあらい水平面の長さだけに比例するので、ばねを縮める長さ x によらず一定である。

　

　

（問5）
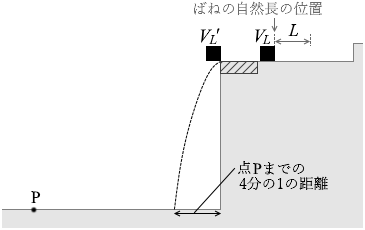速さが VL のままであれば半分の地点まで飛んでいき、速さが VL' になってしまったがために \(\large{\frac{1}{4}}\) の地点までしか飛ばなかったわけですが、問2より、距離が \(\large{\frac{1}{2}}\) であれば飛び出す瞬間の速さも \(\large{\frac{1}{2}}\) であるので、

　　 VL' = \(\large{\frac{1}{2}}\)VL

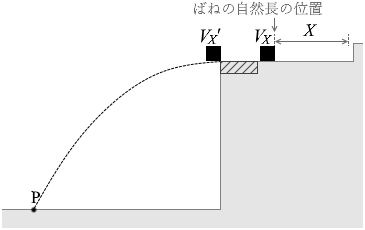速さ VX' で飛び出したときは VL' のときの 4倍飛んでいるので、

　　 VX' = 4VL' = 4×\(\large{\frac{1}{2}}\)VL = 2VL

また、等加速度直線運動の公式より、 (VX')2 - (VX)2 = 2as　であり　(VL')2 - (VL)2 = 2as　であるので、

　　　　(VX')2 - (VX)2 = (VL')2 - (VL)2　　上の結果を代入して

　∴　　(2VL)2 - (VX)2 = (\(\large{\frac{1}{2}}\)VL)2 - (VL)2

　∴　　- (VX)2 = - (2VL)2 + (\(\large{\frac{1}{2}}\)VL)2 - (VL)2

　∴　　- VX2 = - 4VL2 + \(\large{\frac{1}{4}}\)VL2 - VL2

　∴　　- VX2 = - 5VL2 + \(\large{\frac{1}{4}}\)VL2

　∴　　VX2 = 5VL2 - \(\large{\frac{1}{4}}\)VL2

　∴　　VX2 = \(\large{\frac{20-1}{4}}\)VL2

　∴　　 VX = \(\large{\frac{\sqrt{19}}{2}}\)VL

そして、問3より、

　　　　\(\large{\frac{X}{L}}\) = \(\large{\frac{V_X}{V_L}}\)

であり、上の結果より、

　　　　\(\large{\frac{V_X}{V_L}}\) = \(\large{\frac{\sqrt{19}}{2}}\)

であるので、

　　　　 \(\large{\frac{X}{L}}\) = \(\large{\frac{\sqrt{19}}{2}}\)

↑ ↓