(問4)
浮いている物が静止しているとき(=つり合っているとき)というのは、『浮き沈み』で説明したように、浮力と沈ませようとする力の合力が 0(=つり合っている)のときです。
浮力の大きさは ρVg ですが、
ρ の部分は本問では ρ0 で、
V の部分は S×(L - x) です。
すなわち浮力は ρ0S(L - x)g です。
沈ませようとする力は、浮きの重さ ρSLg とおもりの重さ mg の合計であり、
ρSLg + mg です。
この2つの力がつり合っているので、
ρ0S(L - x)g = ρSLg + mg ……①
(あるいは、下向きを正として
- ρ0S(L - x)g + ρSLg + mg = 0
と立式することもできます。)
∴ ρ0S(L - x) = ρSL + m
∴ ρ0SL - ρ0Sx = ρSL + m
∴ - ρ0Sx = - ρ0SL + ρSL + m
∴ ρ0Sx = ρ0SL - ρSL - m
∴ x = L - \(\large{\frac{ρ}{ρ_0}}\)L - \(\large{\frac{m}{ρ_0S}}\)
= (1 - \(\large{\frac{ρ}{ρ_0}}\))L - \(\large{\frac{m}{ρ_0S}}\)
(問5)
運動方程式(ma = F の式)を立てて加速度を求めます。切れた直後の加速度を a と置き、上向きを正とします。
浮きの質量は
ρSL
浮きにはたらく力は
(浮力)-(浮きの重さ)= ρ0S(L - x)g - ρSLg
よって運動方程式は
ρSL × a = ρ0S(L - x)g - ρSLg
この式の右辺に、①を変形した式 ρ0S(L - x)g - ρSLg = mg を代入しますと、
ρSL × a = mg
∴ a = \(\large{\frac{mg}{ρSL}}\)
(余談1)
(問4)の①式 ρ0S(L - x)g = ρSLg + mg を図で表してみますと、
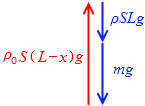 このようになりますが、
このようになりますが、
この状態でつり合っていたものが、急に mg が外されたわけです。外された瞬間、残り2力の合力は、上向きの mg 、というわけです。
つり合っていた状態から突然 f の力を取り除いた瞬間の力は、逆向きの f ということです。
(余談2)
浮力というものは「物体が排除した流体の重さ」であるわけですから、上昇していくうちに浮きが排除する流体の体積は減っていくので、浮力も減っていきます。上昇するにつれて浮きのスピードはゆっくりになっていきます。
水中に完全に潜っている場合は別です。上昇したとしても物体全体がまだ水中にあるうちは排除する流体の体積は変わりませんので。
(余談3)
物理は「静」と「動」に別けて考えると頭の中が整理しやすくなるのですが、まさに(問4)が「静」で(問5)が「動」です。
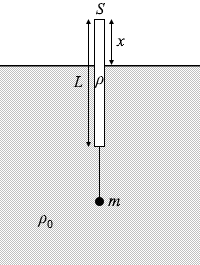
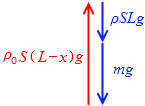 このようになりますが、
このようになりますが、