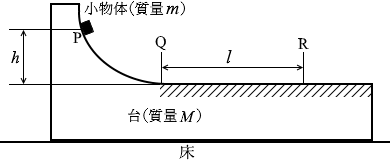
□
図2のように、質量 M の台が水平な床の上に置かれている。この台の上面では、摩擦がない曲面と摩擦がある水平面が点Qで滑らかにつながっている。台の水平面から高さ h にある面上の点Pに質量 m の小物体を置き、静かに放す。ただし、空気による抵抗はなく、重力加速度の大きさを g とする。
図 2
（問3）台が床に固定されているとき、小物体は点Qまで滑り落ちたのち、点Qから距離 l だけ離れた点Rで止まった。QR間の水平面と小物体の間の動摩擦係数 μ' はいくらか。
（問4）次に、台が床の上で摩擦なく自由に動くことができるようにした。台が静止した状態で、点Pから同じ小物体を静かに放した。小物体が台上の点Qに達したときの、小物体の床に対する速度を v 、台の床に対する速度を V とする。ただし、速度は右向きを正とする。このとき、v と V が満たすべき関係式はどれか。正しいものを、次の①～⑧のうちから二つ選べ。ただし、回答の順序は問わない。
① mv + MV = 0 ② mv - MV = 0
③ v + V = 0 ④ v - V = 0
⑤ \(\large{\frac{1}{2}}\)mv 2 = \(\large{\frac{1}{2}}\)MV 2 ⑥ \(\large{\frac{1}{2}}\)mv 2 + \(\large{\frac{1}{2}}\)MV 2 = mgh
⑦ \(\large{\frac{1}{2}}\)mv 2 = mgh ⑧ \(\large{\frac{1}{2}}\)MV 2 = mgh
（問5）問4と同様に台が床の上で摩擦なく自由に動く場合、小物体は、点Qを通り過ぎたのち、点Qからある距離だけ離れた位置で台に対して停止した。この時点における台の床に対する運動はどうなるか。正しいものを、次の①～④のうちから一つ選べ。
① 小物体が停止しても、台は動くが、その進む方向は点Pの高さ h によって決まる。
② 小物体と台の間の摩擦力により、小物体が停止しても台は右向きに進む。
③ 小物体が曲面を下っている間は、台は小物体と反対方向に進むので、小物体が停止しても、慣性の法則により台は左向きに進む。
④ 小物体と台を合わせた全体には水平方向に外力が働かないため、運動量保存の法則により、小物体が停止すると台も停止する。
#センター04本試
（問3）v としますと、力学的エネルギー保存の法則 より、
mgh = \(\large{\frac{1}{2}}\)mv 2 ……➊
（QR間におけるエネルギー保存）摩擦力が仕事をして 運動エネルギーが 0 になっています。摩擦力を F としますと、
0 - \(\large{\frac{1}{2}}\)mv 2 = - Fl
であり、摩擦力 というのは（動摩擦係数）×（垂直抗力）であるので、F = μ' ×mg です。つまり上式は、
- \(\large{\frac{1}{2}}\)mv 2 = - μ'mgl ……➋
です。
（つまり、）
mgh = μ'mgl ……❸
∴ μ' = \(\large{\frac{h}{l}}\)
と求まります。
計算過程を見てみますと \(\large{\frac{1}{2}}\)mv 2 は仮のものであり、求める必要の無いものです。慣れている方はいきなり❸式を立ててしまって構いません。位置エネルギーが摩擦熱に使われた、と考えるのです。
また、 μ' = \(\large{\frac{h}{l}}\) という式を見てみますとこれは『摩擦角 』に似ています。高さ h が大きかったり、長さ l が小さかったりするときは、摩擦が強い、ということです。
（問4）次に、台が床の上で摩擦なく自由に動くことができるようにした。台が静止した状態で、点Pから同じ小物体を静かに放した。小物体が台上の点Qに達したときの、小物体の床に対する速度を v 、台の床に対する速度を V とする。ただし、速度は右向きを正とする。このとき、v と V が満たすべき関係式はどれか。正しいものを、次の①～⑧のうちから二つ選べ。ただし、回答の順序は問わない。
① mv + MV = 0 ② mv - MV = 0
③ v + V = 0 ④ v - V = 0
⑤ \(\large{\frac{1}{2}}\)mv 2 = \(\large{\frac{1}{2}}\)MV 2 ⑥ \(\large{\frac{1}{2}}\)mv 2 + \(\large{\frac{1}{2}}\)MV 2 = mgh
⑦ \(\large{\frac{1}{2}}\)mv 2 = mgh ⑧ \(\large{\frac{1}{2}}\)MV 2 = mgh
（運動量が保存 されているはず）
m ×0 + M ×0 ……❹
点Qでは、小物体は v 、台は V で運動しているから運動量の和は
mv + MV ……❺
運動量保存の法則により ❹ = ❺ であるから、
mv + MV = 0
うっかり mv - MV = 0 としてしまいがちですが、「速度は右向きを正とする。台の床に対する速度を V とする。」と問題文にあるので、これは V 自信が負、という意味であり、MV の前に - を付けるのは間違いです。
（力学的エネルギーも保存 されているはず）
\(\large{\frac{1}{2}}\)m ×02 + mgh + \(\large{\frac{1}{2}}\)M ×02 ……❻
点Qでの力学的エネルギーの和は
\(\large{\frac{1}{2}}\)mv 2 + \(\large{\frac{1}{2}}\)MV 2 ……❼
力学的エネルギー保存の法則より ❻ = ❼ であるから、
\(\large{\frac{1}{2}}\)mv 2 + \(\large{\frac{1}{2}}\)MV 2 = mgh
（というわけで）v と V が満たすべき関係式は ① と ⑥ です。
選択肢のうち
（問5）問4と同様に台が床の上で摩擦なく自由に動く場合、小物体は、点Qを通り過ぎたのち、点Qからある距離だけ離れた位置で台に対して停止した。この時点における台の床に対する運動はどうなるか。正しいものを、次の①～④のうちから一つ選べ。
① 小物体が停止しても、台は動くが、その進む方向は点Pの高さ h によって決まる。
② 小物体と台の間の摩擦力により、小物体が停止しても台は右向きに進む。
③ 小物体が曲面を下っている間は、台は小物体と反対方向に進むので、小物体が停止しても、慣性の法則により台は左向きに進む。
④ 小物体と台を合わせた全体には水平方向に外力が働かないため、運動量保存の法則により、小物体が停止すると台も停止する。
小物体が点Pにいるときは運動量の和が 0 であり、運動量保存の法則により、これはずっと維持されます。点Qにおいても、それ以降においても運動量の和は 0 です。すなわち、小物体が台に対して停止したときは、両方共が停止しないと運動量の和が 0 にならないので、正しい記述は ④ です。
①～③はいずれも台が動くと言っているので間違いです。台が動くなら小物体はその反対方向に動かないと運動量の和が 0 になりえません。台と小物体の間にはたらく摩擦力は内力であり外力ではないので運動量の和に影響しません。
（余談）重心の速度 は保存されます。はじめにその速度が 0 であったので重心の速度はずっと 0 です。動いてません。重心の位置はずっと同じということです。台は少し左に動いて、小物体は大きく右に動きますが、その2つの物体の重心は始めから最後までずっと同じ位置です。
あと、問題文では点Qからどのくらいの距離を滑って止まったのかが書かれてませんが、この距離は l です。問3の❸式 mgh = μ'mgl で示したように、mgh の位置エネルギーを消化するのには l だけ滑らなければなりません。台が動いていても μ'mg の値は変わらないので l の距離が必要です。
↑
↓
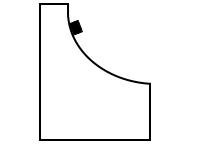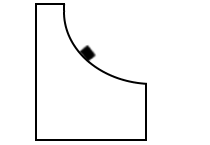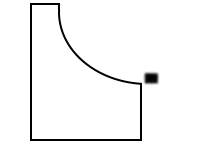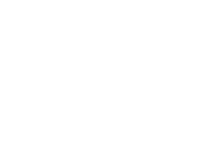台が床の上で摩擦なく自由に動くということは、小物体が点Pから点Qに滑り落ちるときに、台が少し左に動く、ということです。