(問1)V 、v s *
添字の s は sound の頭文字のつもりです。あるいは source です。
閉じる f 0 、f 1 、f 2 、f 3 、b 1 *
beat frequency の頭文字のつもりです。閉じる
ドップラー効果の公式 ( f = \(\large{\frac{V-v_{\rm{o}}}{V-v_{\rm{s}}}}\) f 0 )に代入しますと、
f 1 f 0 = \(\large{\frac{V}{V+v_{\rm{s}}}}\) f 0
f 2 = \(\large{\frac{V-0}{V-(v_{\rm{s}})}}\) f 0 = \(\large{\frac{V}{V-v_{\rm{s}}}}\) f 0
観測者は静止しているので f 2 の振動数をそのまま観測し、
f 3 f 2 = \(\large{\frac{V}{V-v_{\rm{s}}}}\) f 0
f 1 、f 3 をうなりの公式 ( f = | f 1 - f 2 | )に代入しますと、
b 1 f 1 - f 3 | f 1 < f 3 だから*
V も v s も f 1 も f 3 も正であり、分母の形をよく見ますと、f 1 < f 3 であることがわかります。
閉じる
= f 3 - f 1
= \(\large{\frac{V}{V-v_{\rm{s}}}}\normalsize{f_0}\) - \(\large{\frac{V}{V+v_{\rm{s}}}}\) f 0
= \(\big(\large{\frac{V}{V-v_{\rm{s}}}}\) - \(\large{\frac{V}{V+v_{\rm{s}}}})\) f 0
= \(\Big\{\large{\frac{V(V+v_{\rm{s}})}{(V-v_{\rm{s}})(V+v_{\rm{s}})}}\) - \(\large{\frac{(V-v_{\rm{s}})V}{(V-v_{\rm{s}})(V+v_{\rm{s}})}}\)\(\Big\}\) f 0
= \(\large{\frac{V(V+v_{\rm{s}})-(V-v_{\rm{s}})V}{(V-v_{\rm{s}})(V+v_{\rm{s}})}}\) f 0
= \(\large{\frac{V^2+Vv_{\rm{s}}-V^2+Vv_{\rm{s}}}{V^2-v_{\rm{s}}{^2}}}\) f 0
= \(\large{\frac{2Vv_{\rm{s}}}{V^2-v_{\rm{s}}{^2}}}\) f 0
(問2)f 4 、f 5 、b 2 、
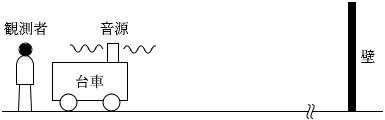
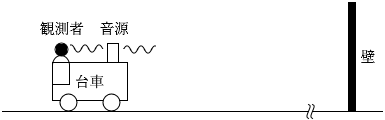
そうしますと、観測者と音源は一緒に動いているので、
f 4 = f 0
壁で観測される超音波の振動数は問1と同じで、
f 2 = \(\large{\frac{V}{V-v_{\rm{s}}}}\) f 0
ですが、今度は観測者が動いているので、さらにドップラー効果が起こり、
f 5 = \(\large{\frac{V-(-v_{\rm{s}})}{V-(0)}}\) f 2
= \(\large{\frac{V+v_{\rm{s}}}{V}}\) f 2
= \(\large{\frac{V+v_{\rm{s}}}{V}}\)⋅\(\large{\frac{V}{V-v_{\rm{s}}}}\) f 0
= \(\large{\frac{V+v_{\rm{s}}}{V-v_{\rm{s}}}}\) f 0
よって、うなりの振動数は
b 2 f 4 - f 5 | f 4 < f 5 だから
= f 5 - f 4
= \(\large{\frac{V+v_{\rm{s}}}{V-v_{\rm{s}}}}\) f 0 - f 0
= \(\large{\frac{(V+v_{\rm{s}})-(V-v_{\rm{s}})}{V-v_{\rm{s}}}}\) f 0
= \(\large{\frac{2v_{\rm{s}}}{V-v_{\rm{s}}}}\) f 0
(2)v s = 2.000 、b 2 = 400 を代入すると、
400 = \(\large{\frac{2×2.000}{V-2.000}}\) f 0
∴ 400V - 800 = 4 f 0 ……①
v s = 9.770 、b 2 = 2000 を代入すると、
2000 = \(\large{\frac{2×9.770}{V-9.770}}\) f 0
∴ 2000V - 19540 = 19.540 f 0 ……②
①を5倍して、
2000V = 20 f 0 + 4000
②式に代入すると、
20 f 0 + 4000 - 19540 = 19.540 f 0
∴ 0.460 f 0 = 15540
∴ f 0 ≒ 33780
これを①式に代入すると、
400V - 800 = 4×33780
∴ 400V = 135120 + 800
∴ 400V = 135920
∴ V = 339.8
答え V = 3.40×102 [m/s] 、f 0 = 3.38×104 [Hz]
(問3)
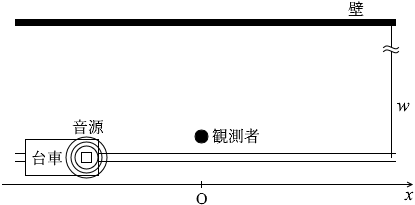
壁で観測される超音波の振動数を f 6 とします。観測者は静止しているので、観測者が観測する振動数も f 6 です。
反射の法則 により入射角と反射角が等しくなっていますが、台車は移動しているので、
θ を定めますと、
v s cosθ の速度で迫ってくることになります。
つまり、壁で観測される超音波の振動数は
f 6 = \(\large{\frac{V-0}{V-v_{\rm{s}}\cosθ}}\) f 0 = \(\large{\frac{V}{V-v_{\rm{s}}\cosθ}}\) f 0 ……③
θ = \(\Large{\frac{\Large{-\frac{x}{2}}}{\sqrt{(-\frac{x}{2})^2+w^2}}}\)
であるとわかります。x の前に - が付くのは、原点Oの左側では x が負であり、長さに直すときはそれに - を付けて正にする必要があるからです)
計算して、
cosθ = \(\Large{\frac{\Large{-\frac{x}{2}}}{\sqrt{(-\frac{x}{2})^2+w^2}}}\) = \(\Large{\frac{\Large{-\frac{x}{2}}×2}{\sqrt{\big\{(-\frac{x}{2})^2+w^2\big\}×4}}}\) = \(\large{\frac{-x}{\sqrt{x^2+4w^2}}}\)
③式に代入しますと、
f 6 = \(\large{\frac{V}{V-v_{\rm{s}}\cosθ}}\) f 0
= \(\large{\frac{V}{V-v_{\rm{s}}\frac{-x}{\sqrt{x^2+4w^2}}}}\) f 0
= \(\large{\frac{V\sqrt{x^2+4w^2}}{V\sqrt{x^2+4w^2}+v_{\rm{s}}x}}\) f 0 ……④
この式を解釈しますと、
x が -∞ に近いときほど、相対的に 4w 2 が 0 に近づき、f 6 は
f 6 = \(\large{\frac{V\sqrt{x^2+0}}{V\sqrt{x^2+0}+v_{\rm{s}}x}}\) f 0
= \(\large{\frac{V|x|}{V|x|+v_{\rm{s}}x}}\) f 0 (|x | で割りますと、x は負だから)
= \(\large{\frac{V}{V-v_{\rm{s}}}}\) f 0
に近づきます。
x が +∞ に近いときも、相対的に 4w 2 が 0 に近づき、f 6 は
f 6 = \(\large{\frac{V\sqrt{x^2+0}}{V\sqrt{x^2+0}+v_{\rm{s}}x}}\) f 0
= \(\large{\frac{V|x|}{V|x|+v_{\rm{s}}x}}\) f 0 (|x | で割りますと、x は正だから)
= \(\large{\frac{V}{V+v_{\rm{s}}}}\) f 0
に近づきます。
x が 0 のときは、
f 6 = \(\large{\frac{V\sqrt{x^2+4w^2}}{V\sqrt{x^2+4w^2}-v_{\rm{s}}x}}\) f 0 = \(\large{\frac{V\sqrt{0^2+4w^2}}{V\sqrt{0^2+4w^2}-v_{\rm{s}}⋅0}}\) f 0 = \(\large{\frac{V\sqrt{4w^2}}{V\sqrt{4w^2}}}\) f 0 = f 0
です。
そして、x が -∞ 、+∞ に近いときは変化量が小さく、x が 0 に近いときは変化量が大きいです。
つまり、グラフは以下のようになります。
(正負がややこしい)
θ をこのように定めたということは、
x > 0 においては cosθ は負になる*
たとえば cos120° = cos(180°-60°) = - cos60°
閉じる v s cosθ は壁から遠ざかる方向になるということです。
このことを踏まえてあらためて④式を見てみますと、
f 6 = \(\large{\frac{V}{V-v_{\rm{s}}\cosθ}}\) f 0
= \(\large{\frac{V}{V-v_{\rm{s}}\frac{-x}{\sqrt{x^2+4w^2}}}}\) f 0
= \(\large{\frac{V\sqrt{x^2+4w^2}}{V\sqrt{x^2+4w^2}+v_{\rm{s}}x}}\) f 0
x < 0 のときは cosθ > 0 で、分母の v s x の前の符号は - になり、x > 0 のときは cosθ < 0 で、分母の v s x の前の符号は + になる、と整合性が取れていることが確認できます。
もし、x < 0 のときが cosθ > 0 で、x > 0 のときが cosθ < 0 であることが気持ち悪いというのであれば、
θ を左図のように設定すれば、x が - ∞ のときに cosθ が - 1 で、x が + ∞ のときに cosθ が + 1 になって、いい感じになります。でも問題に慣れてないとなかなか気付けません。
いずれにしても、x が - ∞ のときの振動数は
f 6 = \(\large{\frac{V}{V-v_{\rm{s}}}}\) f 0
で、x が + ∞ のときの振動数は
f 6 = \(\large{\frac{V}{V+v_{\rm{s}}}}\) f 0
となり、正負がややこしい中でミスを防ぐには「音源が近づいてくるときは分母が引き算、音源が遠ざかるときは分母が足し算」としっかり覚えておくことが重要です。
 反射する波は
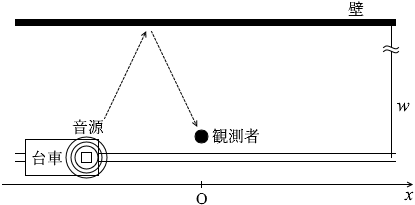
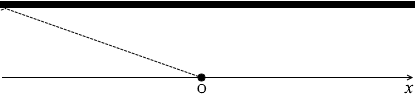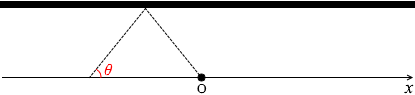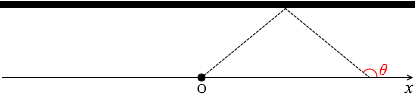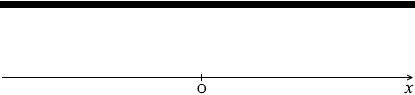
反射する波は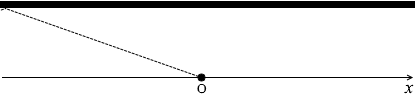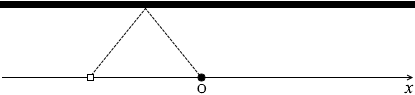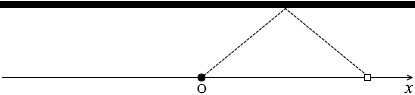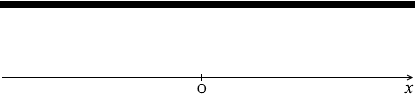 反射して観測者に届く超音波の経路は左図のようになります。
反射して観測者に届く超音波の経路は左図のようになります。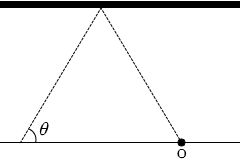 左図のように θ を定めますと、
左図のように θ を定めますと、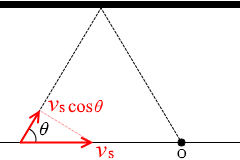 壁にとっては音源が vscosθ の速度で迫ってくることになります。
壁にとっては音源が vscosθ の速度で迫ってくることになります。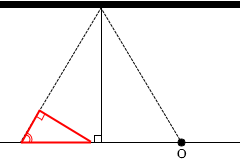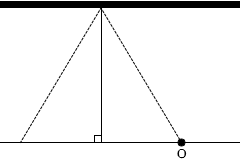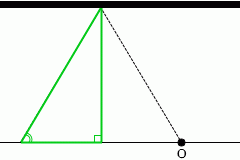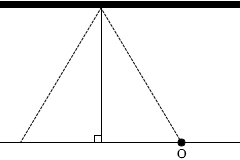 ところで、左図の赤色三角形と緑色三角形は、2つの角の大きさが同じなので相似であり、
ところで、左図の赤色三角形と緑色三角形は、2つの角の大きさが同じなので相似であり、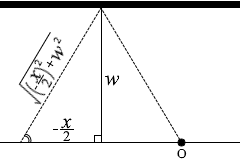 cosθ = \(\Large{\frac{\Large{-\frac{x}{2}}}{\sqrt{(-\frac{x}{2})^2+w^2}}}\)
cosθ = \(\Large{\frac{\Large{-\frac{x}{2}}}{\sqrt{(-\frac{x}{2})^2+w^2}}}\)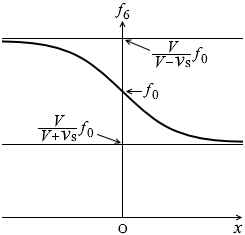
 このようであるということであり、
このようであるということであり、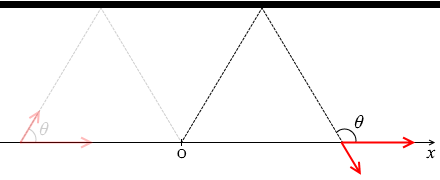 x > 0 においては cosθ は負になる
x > 0 においては cosθ は負になる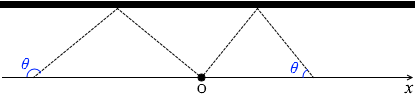 θ を左図のように設定すれば、x が - ∞ のときに cosθ が - 1 で、x が + ∞ のときに cosθ が + 1 になって、いい感じになります。でも問題に慣れてないとなかなか気付けません。
θ を左図のように設定すれば、x が - ∞ のときに cosθ が - 1 で、x が + ∞ のときに cosθ が + 1 になって、いい感じになります。でも問題に慣れてないとなかなか気付けません。