音のドップラー効果について考える。音源、観測者、反射板はすべて一直線上に位置しているものとし、空気中の音の速さは V とする。また、風は吹いていないものとする。
(問1)次の文章中の空欄ア・イに入れる語句と式の組合せとして最も適当なものを、下の①~⑨のうちから一つ選べ。
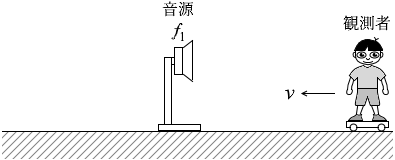
図1のように、静止している振動数 f1 の音源へ向かって、観測者が速さ v で移動している。このとき、観測者に聞こえる音の振動数はア、音源から観測者へ向かう音波の波長はイである。
| ア | イ | |
|---|---|---|
| ① | f1 よりも小さく | \(\large{\frac{V-v}{f_1}}\) |
| ② | f1 よりも小さく | \(\large{\frac{V}{f_1}}\) |
| ③ | f1 よりも小さく | \(\large{\frac{V^2}{(V+v)f_1}}\) |
| ④ | f1 と等しく | \(\large{\frac{V-v}{f_1}}\) |
| ⑤ | f1 と等しく | \(\large{\frac{V}{f_1}}\) |
| ⑥ | f1 と等しく | \(\large{\frac{V^2}{(V+v)f_1}}\) |
| ⑦ | f1 よりも大きく | \(\large{\frac{V-v}{f_1}}\) |
| ⑧ | f1 よりも大きく | \(\large{\frac{V}{f_1}}\) |
| ⑨ | f1 よりも大きく | \(\large{\frac{V^2}{(V+v)f_1}}\) |
(問2)図2のように、静止している観測者へ向かって、振動数 f2 の音源が速さ v で移動している。音源から観測者へ向かう音波の波長 λ を式で表わせ。

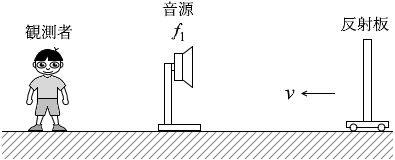
(問3)図3のように、静止している振動数 f1 の音源へ向かって、反射板を速さ v で動かした。音源の背後で静止している観測者は、反射板で反射した音を聞いた。その音の振動数は f3 であった。反射板の速さ v を式で表わせ。
#センター17本試物理
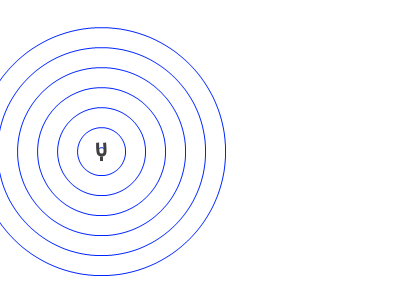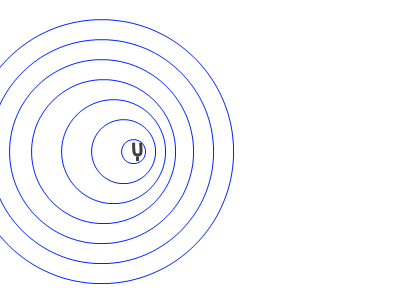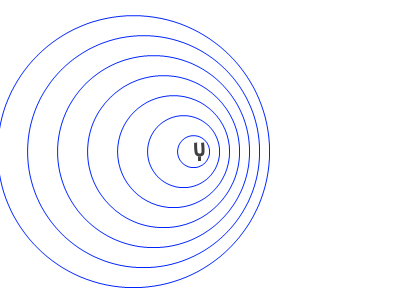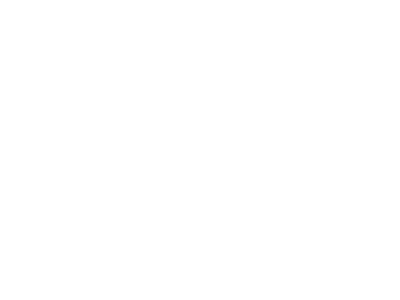 これは音源が動いているような場合ではなく、
これは音源が動いているような場合ではなく、
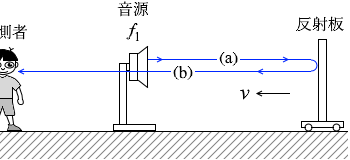 入射波を(a)、反射波を(b)として分けて考えてみます。
入射波を(a)、反射波を(b)として分けて考えてみます。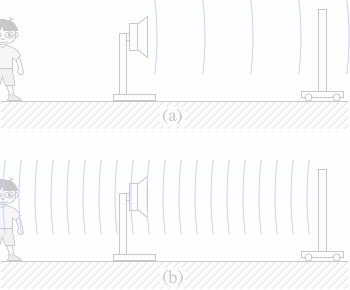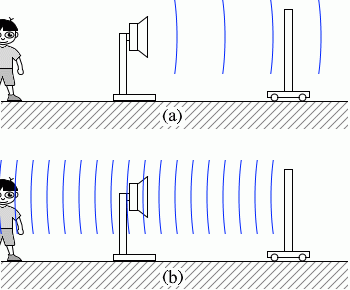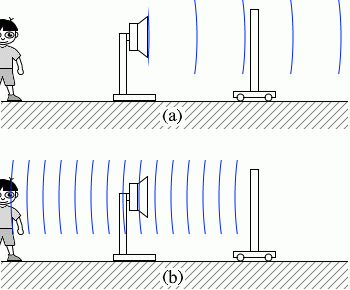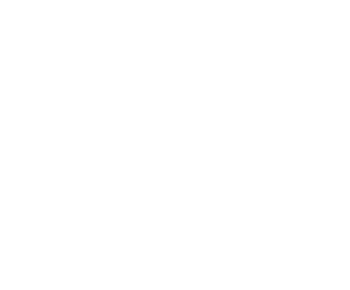 反射板は、青波がぶつかってきた瞬間に青波を発射します。
反射板は、青波がぶつかってきた瞬間に青波を発射します。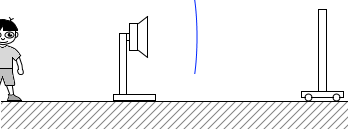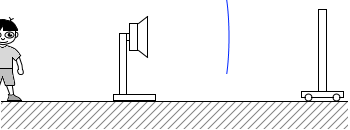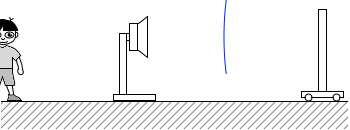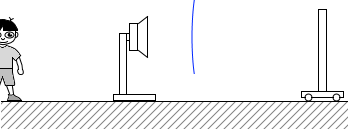 空気中を進む音波の速さは
空気中を進む音波の速さは