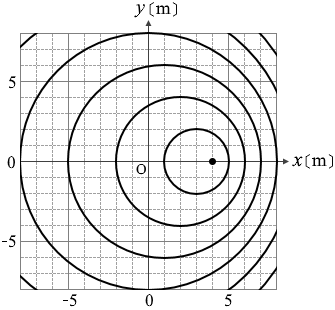
図3は、流れのない媒質中を動く波源がつくる波の様子を示している。波源は一定の速さ 0.5m/s で x軸上を右方向に進み、波は xy平面において一定の速さで円形に広がる。図中の黒丸と曲線はそれぞれ、ある時刻における波源の位置と波の山の位置を表している。
(問3)この波源の振動の周期はいくらか。
(問4)x軸上における媒質の振動の周期を、波源の位置より左側で T1 、右側で T2 とする。周期の比 \(\large{\frac{T_2}{T_1}}\) はいくらか。
#センター16追試物理
図3は、流れのない媒質中を動く波源がつくる波の様子を示している。波源は一定の速さ 0.5m/s で x軸上を右方向に進み、波は xy平面において一定の速さで円形に広がる。図中の黒丸と曲線はそれぞれ、ある時刻における波源の位置と波の山の位置を表している。

(問3)この波源の振動の周期はいくらか。
(問4)x軸上における媒質の振動の周期を、波源の位置より左側で T1 、右側で T2 とする。周期の比 \(\large{\frac{T_2}{T_1}}\) はいくらか。
#センター16追試物理
(問3)
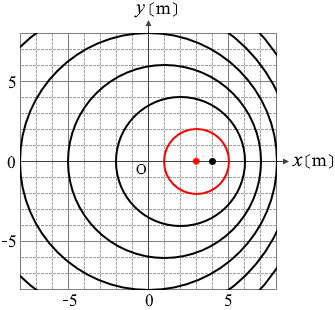 波は円形に広がっていくので左図の赤波が発射された地点は円の中心、左図の赤丸の地点です。
波は円形に広がっていくので左図の赤波が発射された地点は円の中心、左図の赤丸の地点です。
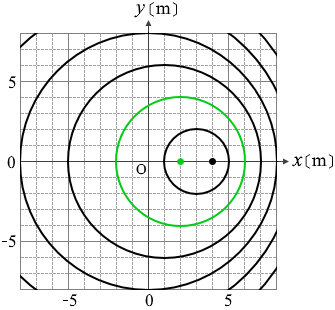 左図の緑波については緑点。
左図の緑波については緑点。
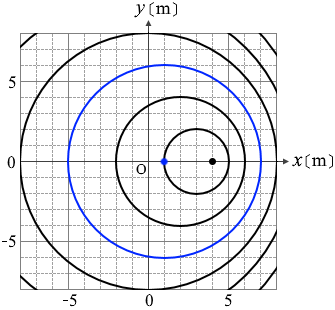 以下同様。
以下同様。
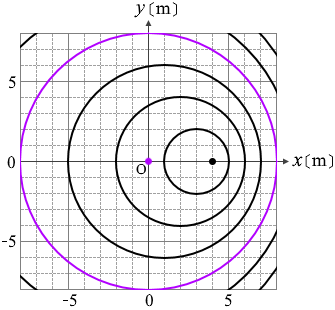
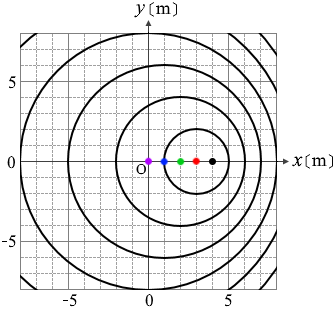 発射地点をまとめて描きますと左図のようになり、これが波源の動きということになります。この波源は 0.5m/s で進んでいて、1m おきに波は発射されていますから、波は 2s おきに発射されているということになります。
発射地点をまとめて描きますと左図のようになり、これが波源の動きということになります。この波源は 0.5m/s で進んでいて、1m おきに波は発射されていますから、波は 2s おきに発射されているということになります。
この波源の振動の周期は 2s です。
(問4)
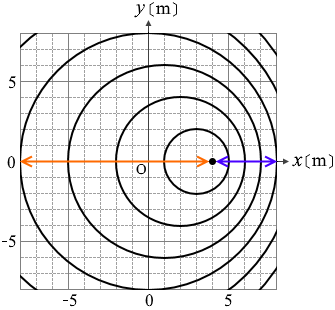 波源の左側 ↔ では波の間隔が大きくなっていて、波源の右側 ↔ では波の間隔が小さくなっていて、この問題はまさにドップラー効果の問題ですが、ドップラー効果の式を使わずに解いてみます。
波源の左側 ↔ では波の間隔が大きくなっていて、波源の右側 ↔ では波の間隔が小さくなっていて、この問題はまさにドップラー効果の問題ですが、ドップラー効果の式を使わずに解いてみます。
まず、波のスピードを求めてみます。波の円が大きくなっていくスピードです。波源のスピードではありません。
 左図の瞬間の 2s 前には
左図の瞬間の 2s 前には
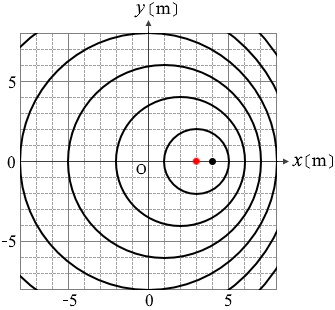 波源はここにいたわけです。(波源のスピードは 0.5m/s ですから)
波源はここにいたわけです。(波源のスピードは 0.5m/s ですから)
 そして 2s 後にはこの形になっているわけですから
そして 2s 後にはこの形になっているわけですから
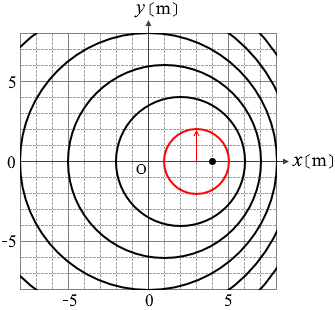 波のスピードは 2m/2s = 1 m/s ということになります。
波のスピードは 2m/2s = 1 m/s ということになります。
この波のスピードは波源の左側 ↔ でも波源の右側 ↔ でも変わりません。
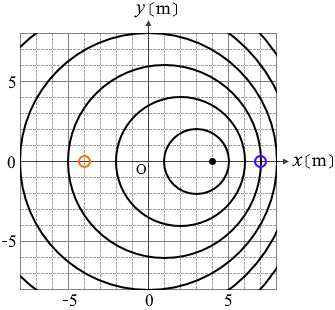 波源の左側では波の間隔は 3m であり、観測者○が感知する周期は T1 = 3 s ということになります。同様に、波源の右側では波の間隔は 1m であり、観測者○が感知する周期は T2 = 1 s ということになります。
波源の左側では波の間隔は 3m であり、観測者○が感知する周期は T1 = 3 s ということになります。同様に、波源の右側では波の間隔は 1m であり、観測者○が感知する周期は T2 = 1 s ということになります。
よって、
\(\large{\frac{T_2}{T_1}}\) = \(\large{\frac{1}{3}}\)
(別解:波のスピードを求めなくても)
波のスピードは波源の左側でも右側でも同じであり、これを V と置いて(v = \(\large{\frac{λ}{T}}\)
波の基本式
f = \(\large{\frac{1}{T}}\)
v = fλ
より
v = \(\large{\frac{λ}{T}}\)
の式を立てますと)
V = \(\large{\frac{λ_1}{T_1}}\)
V = \(\large{\frac{λ_2}{T_2}}\)
⇒
V = \(\large{\frac{3}{T_1}}\)
V = \(\large{\frac{1}{T_2}}\)
ゆえに、
\(\large{\frac{T_2}{T_1}}\) = \(\large{\frac{\frac{1}{V}}{\frac{3}{V}}}\) = \(\large{\frac{1}{3}}\)
と求められます。
…といいますか、
「波のスピードは波源の左側でも右側でも同じであり、左側に比べて右側は波の細かさが \(\large{\frac{1}{3}}\) なのだから周期も \(\large{\frac{1}{3}}\) 」
と暗算で求められます。
(別解:ドップラー効果の式を使う)
波源の左側についてドップラー効果の式を立てますと、
f1 = \(\large{\frac{1}{1+0.5}}\)f0 = \(\large{\frac{2}{3}}\)f0
同様に右側についてはf2 = \(\large{\frac{1}{1-0.5}}\)f0 = 2f0
周期は振動数の逆数だから、
T1 = \(\large{\frac{3}{2f_0}}\)
T2 = \(\large{\frac{1}{2f_0}}\)
ゆえに、
\(\large{\frac{T_2}{T_1}}\) = \(\large{\frac{\frac{1}{2f_0}}{\frac{3}{2f_0}}}\) = \(\large{\frac{1}{3}}\)
と求められます。が、ドップラー効果の式は正負や分母分子を間違えたりしやすいのでなるべく使わない方がいいです。
(余談)
 波源の右側にいる○の観測者も波源に追い越されれば○の立場になります。
波源の右側にいる○の観測者も波源に追い越されれば○の立場になります。
(分かりきったことだと思いますが念のため)