(問1)屈折の法則(スネルの法則) より、*
\(\Large{\frac{\sin i}{\sin r}}\) = \(\Large{\frac{v_1}{v_2}}\) = \(\large{\frac{\lambda_1}{\lambda_2}}\) = n 12
閉じる
\(\large{\frac{L}{l}}\)
(これは分母と分子をとても間違えやすいです)
(問2)l に比べて大きいときは反射波の様子は左図のようになります。
l に比べて小さいときは左図のようになります。
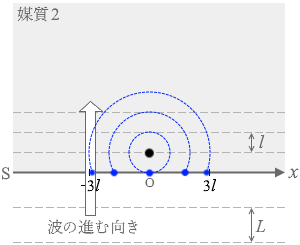
l に比べて十分小さいときは左図のようになります。同心円状です。
*
l というわけではありません。閉じる
(良問)
それにしてもこれはホイヘンスの原理 をちゃんと理解しているかを問う良い問題です。
(問3)
d + \(\sqrt{x^2+d^2}\)
であり、
スタートラインにいる平面波の経路の長さは 0 であるので、
両者の経路差は
d + \(\sqrt{x^2+d^2}\)
であり、この差が波長 l の n 倍であれば強め合う ので、
d + \(\sqrt{x^2+d^2}\) = nl
(実際の様子)
(問4)x と d をそれぞれ横軸と縦軸にとり、
d ≦ \(\large{\frac{5}{2}}\)l と - 3l ≦ x ≦ 3l の範囲で、
間3で求めた条件式
d + \(\sqrt{x^2+d^2}\) = nl
のグラフを描けということなので、
上式を変形して、
\(\sqrt{x^2+d^2}\) = nl - d
∴ x 2 + d 2 = (nl - d )2
∴ x 2 + d 2 = (nl )2 - 2dnl + d 2
∴ x 2 = (nl )2 - 2dnl
∴ 2dnl = - x 2 + (nl )2
∴ d = - \(\large{\frac{1}{2nl}}\)x 2 + \(\large{\frac{nl}{2}}\) ……①
この関数の曲線は上に凸の放物線になりますが、具体的に n の値を代入してみますと、
n = 1 のとき、d = - \(\large{\frac{1}{2l}}\)x 2 + \(\large{\frac{1}{2}}\)l
x = 0 のとき d = \(\large{\frac{1}{2}}\)l 、d = 0 のとき x = l
n = 2 のとき、d = - \(\large{\frac{1}{4l}}\)x 2 + l
x = 0 のとき d = l 、d = 0 のとき x = 2l
n = 3 のとき、d = - \(\large{\frac{1}{6l}}\)x 2 + \(\large{\frac{3}{2}}\)l
x = 0 のとき d = \(\large{\frac{3}{2}}\)l 、d = 0 のとき x = 3l
n = 4 のとき、d = - \(\large{\frac{1}{8l}}\)x 2 + 2l ……②
x = 0 のとき d = 2l 、d = 0 のとき x = 4l
n = 5 のとき、d = - \(\large{\frac{1}{10l}}\)x 2 + \(\large{\frac{5}{2}}\)l ……③
x = 0 のとき d = \(\large{\frac{5}{2}}\)l 、d = 0 のとき x = 5l
よってグラフの概形は以下のようになります。
(図1でいいますと)
d ≒ 0 のときは左図のような感じで、*
閉じる
d = l のときは左図のような感じです。*
閉じる
(問5)d = \(\large{\frac{15}{8}}\)l の線を描き込むと左図のようになりますので、強め合う干渉点が存在するのは n = 4, 5 の場合のみです。
n = 6 の場合も考えてみますと、問4の①式は
d = - \(\large{\frac{1}{12l}}\)x 2 + 3l
x = 0 のとき d = 3l 、d = 0 のとき x = 6l
x = 3l のとき d = \(\large{\frac{9}{4}}\)l
よって、赤線とは交差しません。
というわけで、n = 4, 5 の放物線が赤線と交わるときの x の値を求めると、
②式と d = \(\large{\frac{15}{8}}\)l より、
\(\large{\frac{15}{8}}\)l = - \(\large{\frac{1}{8l}}\)x 2 + 2l
∴ 15l 2 = - x 2 + 16l 2
∴ x 2 = l 2
∴ x = ± l
③式と d = \(\large{\frac{15}{8}}\)l より、
\(\large{\frac{15}{8}}\)l = - \(\large{\frac{1}{10l}}\)x 2 + \(\large{\frac{5}{2}}\)l
∴ \(\large{\frac{15}{8}}\)l ×40l = - \(\large{\frac{1}{10l}}\)x 2 ×40l + \(\large{\frac{5}{2}}\)l ×40l
∴ 75l 2 = - 4x 2 + 100l 2
∴ 4x 2 = 25l 2
∴ x = ± \(\large{\frac{5}{2}}\)l
よって、
x = ± l , ± \(\large{\frac{5}{2}}\)l
(この値は)d -x グラフでいうと左図のような点であり、
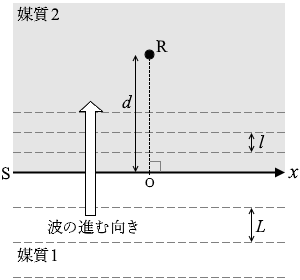
 反射体の直径が l に比べて大きいときは反射波の様子は左図のようになります。
反射体の直径が l に比べて大きいときは反射波の様子は左図のようになります。 直径が l に比べて小さいときは左図のようになります。
直径が l に比べて小さいときは左図のようになります。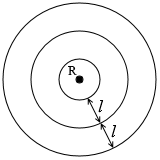 直径が l に比べて十分小さいときは左図のようになります。同心円状です。
直径が l に比べて十分小さいときは左図のようになります。同心円状です。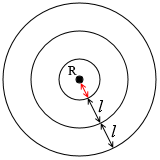
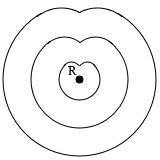 波面がハート型になると考えたり、
波面がハート型になると考えたり、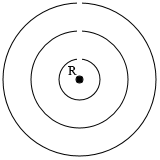 隙間が空くと考えたりしてはダメです。ホイヘンスの原理を理解してないことになります。
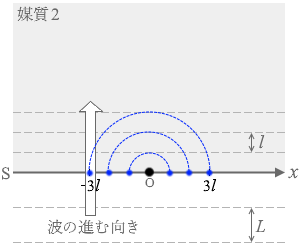
隙間が空くと考えたりしてはダメです。ホイヘンスの原理を理解してないことになります。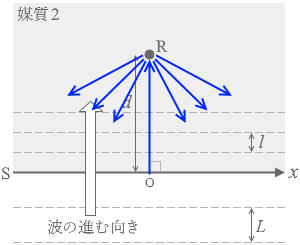 境界面Sをスタートラインと呼びますと、スタートラインの原点Oから出発した波がRで反射してまた戻ってきて、スタートラインにいる波と干渉するわけですが、
境界面Sをスタートラインと呼びますと、スタートラインの原点Oから出発した波がRで反射してまた戻ってきて、スタートラインにいる波と干渉するわけですが、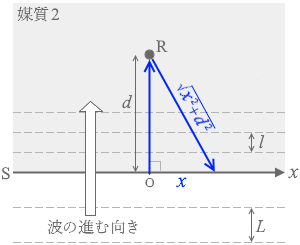 反射波がスタートラインまで戻ってくるまでの経路の長さは
反射波がスタートラインまで戻ってくるまでの経路の長さは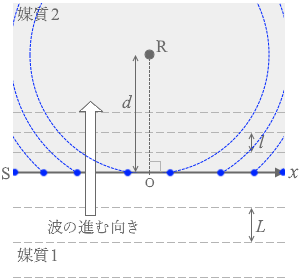
 x と d をそれぞれ横軸と縦軸にとり、
x と d をそれぞれ横軸と縦軸にとり、 0 < d ≦ \(\large{\frac{5}{2}}\)l と - 3l ≦ x ≦ 3l の範囲で、
0 < d ≦ \(\large{\frac{5}{2}}\)l と - 3l ≦ x ≦ 3l の範囲で、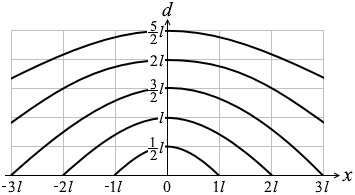
 d ≒ 0 のときは左図のような感じで、
d ≒ 0 のときは左図のような感じで、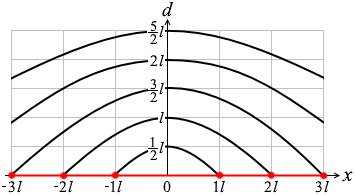
 d = l のときは左図のような感じです。
d = l のときは左図のような感じです。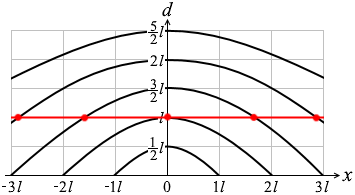
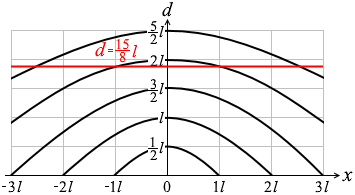 問4のグラフに d = \(\large{\frac{15}{8}}\)l の線を描き込むと左図のようになりますので、強め合う干渉点が存在するのは n = 4, 5 の場合のみです。
問4のグラフに d = \(\large{\frac{15}{8}}\)l の線を描き込むと左図のようになりますので、強め合う干渉点が存在するのは n = 4, 5 の場合のみです。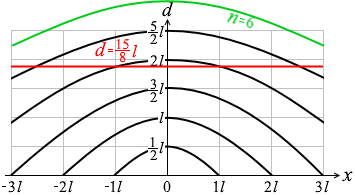 いちおう n = 6 の場合も考えてみますと、問4の①式は
いちおう n = 6 の場合も考えてみますと、問4の①式は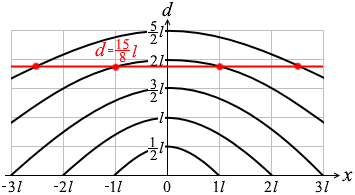 d-xグラフでいうと左図のような点であり、
d-xグラフでいうと左図のような点であり、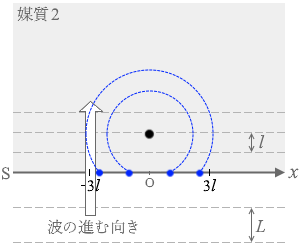 図1でいうと左図のような点です。
図1でいうと左図のような点です。