池に潜り、深さ h の位置から水面を見上げ、水の外を見ていた。図3のように、光を通さない円板が水面に置かれたので、外が全く見えなくなった。そのとき円板の中心は、潜っている人の目の鉛直上方にあった。このように外が見えなくなる円板の半径の最小値 R はいくらか。ただし、空気に対する水の屈折率(相対屈折率)を n とし、水面は波立っていないものとする。また、円板の厚さと目の大きさは無視してよい。
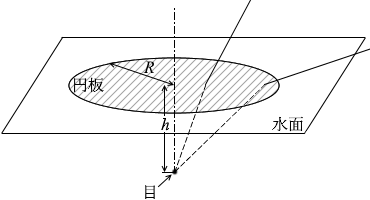
#センター09本試
池に潜り、深さ h の位置から水面を見上げ、水の外を見ていた。図3のように、光を通さない円板が水面に置かれたので、外が全く見えなくなった。そのとき円板の中心は、潜っている人の目の鉛直上方にあった。このように外が見えなくなる円板の半径の最小値 R はいくらか。ただし、空気に対する水の屈折率(相対屈折率)を n とし、水面は波立っていないものとする。また、円板の厚さと目の大きさは無視してよい。

#センター09本試
(外が全く見えなくなった)
というのは、
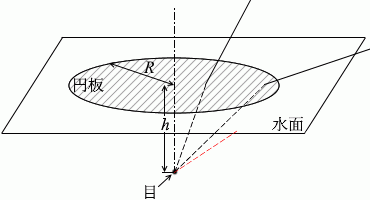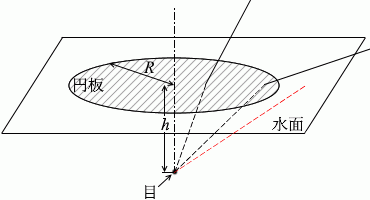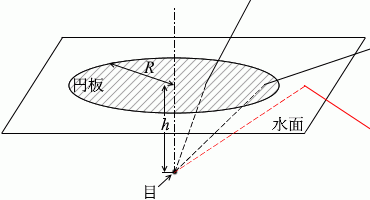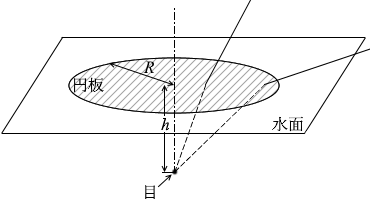 円板の外に目線をやっても全反射が起きて水面上部が見えなくなった、という意味です。
円板の外に目線をやっても全反射が起きて水面上部が見えなくなった、という意味です。
厳密なことを言えば、
まわりの風景の光が目に入り込んでくるわけですから、
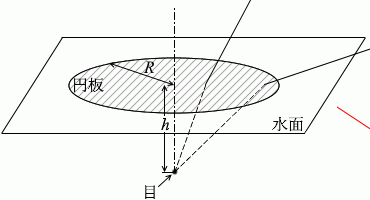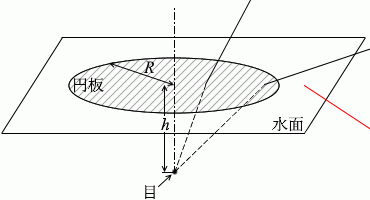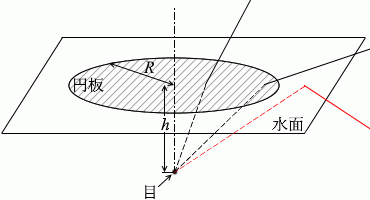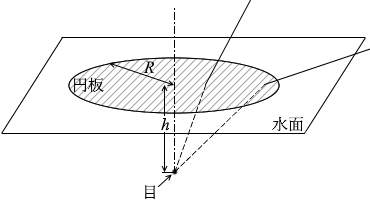 このように描くべきかもしれませんが、
このように描くべきかもしれませんが、
光の逆行により、向こうから入ってくる光もこちらから進んでいく光も同じ経路をたどるので、
どっちにしろ一緒です。
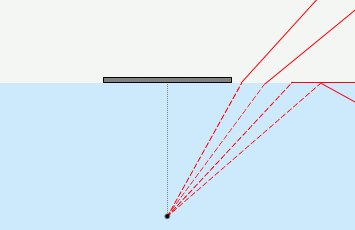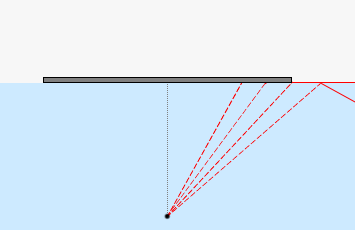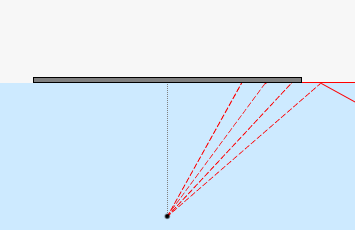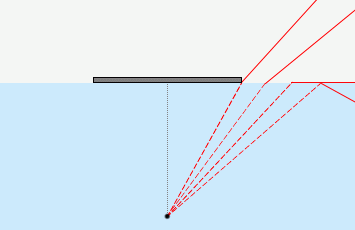 この全反射が起こる臨界角を探れ、というのが本問の主旨です。
この全反射が起こる臨界角を探れ、というのが本問の主旨です。
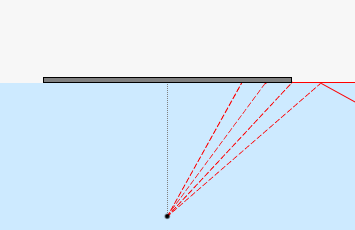 臨界角となるポイントまでの範囲を覆えばそれ以上は覆う必要はありません。この領域さえ覆ってしまえば、水中の人は水上の世界が見えなくなります。船のすぐ真下に潜り込んだダイバーは上の世界が全く見えなくなります。
臨界角となるポイントまでの範囲を覆えばそれ以上は覆う必要はありません。この領域さえ覆ってしまえば、水中の人は水上の世界が見えなくなります。船のすぐ真下に潜り込んだダイバーは上の世界が全く見えなくなります。
(臨界角 i0 は)
sini0 = n12 = \(\large{\frac{n_2}{n_1}}\)
でありますが、これは媒質1から媒質2に向かうときの屈折率のことです。問題文で与えられている n という量は空気に対する水の屈折率(相対屈折率
実質的には絶対屈折率でありますが。
真空と空気は絶対屈折率がほぼ同じとみなせるので。
)であって、これは空気から水に向かうときの屈折率です。ですから、水から空気に向かうときの屈折率は \(\large{\frac{1}{n}}\) ということになります。すなわち、
sini0 = \(\large{\frac{1}{n}}\) ……①
です。
n なのか \(\large{\frac{1}{n}}\) なのかは非常に間違いやすいポイントです。
うっかりミス予防のため「sini0 は 1 より大きくならない」ということを覚えておいてください。
屈折率(絶対屈折率)というのは、空気(真空)が 1.00 で、他は皆1.00以上の値です。水は 約1.33 です。本問で与えられている n は具体的には 約1.33 です。
sini0 = n なのか sini0 = \(\large{\frac{1}{n}}\) なのか迷った場合は、具体的に 1.33 を代入してみて sini0 がちゃんと1以下になっているか確かめてください。sini0 = 1.33 はおかしいです。 sini0 = \(\large{\frac{1}{1.33}}\) ならおかしくないです。
(図を使って sini0 を考える)
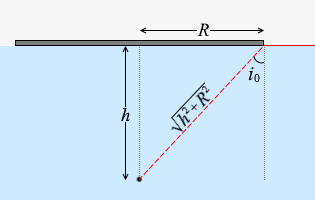 三平方の定理より、斜めの部分の長さは \(\sqrt{h^2+R^2}\)
三平方の定理より、斜めの部分の長さは \(\sqrt{h^2+R^2}\)
であるので、
sini0 = \(\large{\frac{R}{\sqrt{h^2+R^2}}}\) ……②
です。
①、②より、
\(\large{\frac{R}{\sqrt{h^2+R^2}}}\) = \(\large{\frac{1}{n}}\)
∴ nR = \(\sqrt{h^2+R^2}\)
∴ n2R2 = h2 + R2
∴ (n2 - 1)R2 = h2
∴ R2 = \(\large{\frac{h^2}{n^2-1}}\)
∴ R = \(\large{\frac{h}{\sqrt{n^2-1}}}\)