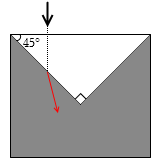
直方体の容器をある透明な液体で満たした後、屈折率が 2.0 の透明な素材でできた直角プリズムで図4のようにふたをした。図のように真上から光線が入射したとき、液体の屈折率 n がある条件を満たすならば、プリズムと液体の境界で光がすべて反射される。この条件として最も適当なものを、下の①~⑥のうちから一つ選べ。

① n < 1.4 ② n > 1.4 ③ n < 2.0 ④ n > 2.0 ⑤ n < 2.8 ⑥ n > 2.8
#センター08追試
直方体の容器をある透明な液体で満たした後、屈折率が 2.0 の透明な素材でできた直角プリズムで図4のようにふたをした。図のように真上から光線が入射したとき、液体の屈折率 n がある条件を満たすならば、プリズムと液体の境界で光がすべて反射される。この条件として最も適当なものを、下の①~⑥のうちから一つ選べ。

① n < 1.4 ② n > 1.4 ③ n < 2.0 ④ n > 2.0 ⑤ n < 2.8 ⑥ n > 2.8
#センター08追試
題意がちょっと分かりづらいと思いますが、これは直方体の容器に液体を満たした後、上からプリズムでふたをしたということです。当然ふたをしたときは液体がこぼれ落ちたはずです。
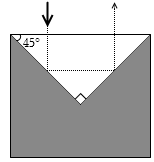 反射の法則により 入射角 = 反射角 です。45° の角度がついていることによって、光線は2度反射し、ちょうど真上に戻っていきます。
このとき角度が 60° であったりすると
反射の法則により 入射角 = 反射角 です。45° の角度がついていることによって、光線は2度反射し、ちょうど真上に戻っていきます。
このとき角度が 60° であったりすると
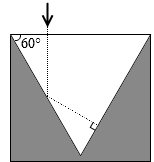
光線は真上に戻っていきません。
このとき光線が液体の中に進まずに全反射する条件を求めよというのが問題の主旨です。
『全反射』項で説明したように全反射というのは屈折率の大きい媒質から小さい媒質へ進むときに起こるものです。屈折率の小さい媒質から大きい媒質へ進むときは起こりません。
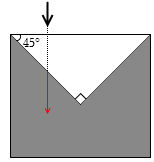 また、同じ屈折率の媒質同士ではそもそも屈折が起こりません。光線はそのまま真っ直ぐ進みます。
また、同じ屈折率の媒質同士ではそもそも屈折が起こりません。光線はそのまま真っ直ぐ進みます。
 さらに、例えば屈折率 2.0 のプリズムから屈折率 1.9 の液体へ進む場合など、屈折率にあまり差がなければ曲がる角度も小さいです。
さらに、例えば屈折率 2.0 のプリズムから屈折率 1.9 の液体へ進む場合など、屈折率にあまり差がなければ曲がる角度も小さいです。
全反射が起こるのは屈折率にしっかり差があるときです 入射角がとても大きいときは別ですが。 。
(ここまでのことを理解していれば直感的に正解は①であるとわかると思います。)
全反射がぎりぎり起こる場合の液体の屈折率を n2 と置きます。
臨界角は
sini0 = \(\large{\frac{n_2}{n_1}}\)
という式で表されますが、ここに i0 = 45° 、n1 = 2.0 を代入しますと、
sin45° = \(\large{\frac{n_2}{2.0}}\)
∴ \(\large{\frac{1}{\sqrt{2}}}\) = \(\large{\frac{n_2}{2.0}}\)
∴ n2 = \(\large{\frac{2.0}{\sqrt{2}}}\) = \(\sqrt{2}\) ≒ 1.4142
n が n2 より小さければ、すなわち n < 1.4 であれば、全反射が起こります。
答えは ① です。