次の文章中の空欄ウ⋅エに入れる数値および語句の組合せとして最も適当なものを、下の①～④のうちから一つ選べ。
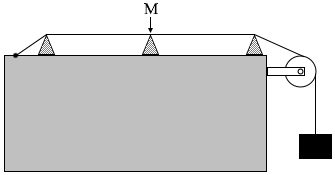
図5のように、張力が一定になるように弦を張り、その中点Mに可動式のコマを置いて、二つの部分に分割した。両側の弦をはじくと、同じ基本振動数の音が聞こえた。この振動数は、中点Mのコマがない場合に弦をはじいて得られる基本振動数のウ倍である。
次に、コマを中点Mから右に少しずれた場所に動かして、両側の弦をはじくと、それぞれの基本振動数の音が重なって、うなりが聞こえた。コマをずらして、中点Mからさらに遠ざけると、うなりの周期はエなった。
| ウ | エ | |
|---|---|---|
| ① | 2 | 長く |
| ② | \(\frac{1}{2}\) | 長く |
| ③ | 2 | 短く |
| ④ | \(\frac{1}{2}\) | 短く |
#センター14本試
ウ
弦の固有振動数は
fn = \(\large{\frac{n}{2l}\sqrt{\frac{S}{\rho}}}\)
という式で表されますが、今は基本振動数について問われているので、
f1 = \(\large{\frac{1}{2l}\sqrt{\frac{S}{\rho}}}\)
です。弦の長さ l に反比例し、弦の張力 S の平方根に比例し、線密度 ρ の平方根に反比例します。本問では張力と線密度が一定で弦の長さが半分であるから、基本振動数は 2 倍です。
ギターをやっている人は、弦を短くすると音（振動数）が高くなるのはよく知っていると思います。
エ
うなりの振動数は
f = | f1 - f2 |
と表されますが、これは、異なる2つの振動数の差が大きいほど、うなりの振動数も大きいということを表しています。
コマを中点Mから徐々に遠ざけると、2つの弦の長さの差が大きくなっていくので振動数の差も大きくなっていきます。つまり、うなりの振動数は大きくなっていきます。
そして、振動数というのは周期の逆数であるので、うなりの振動数が大きくなっていけば、うなりの周期は 短く なっていきます。
というわけで答えは ③ です。