（問1）
ア
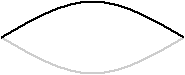弦の基本振動というのはこのような振動のことですが、
弦の長さが 0.450m ということなので、この振動が起こっているときの
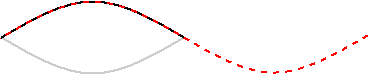波長の大きさは弦の長さの2倍の 0.900m です。
波の速さは振動数と波長を掛けたものだから、
360 × 0.900 = 324 [m/s]
イ
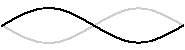腹が二つの定常波ができるということは振動が2倍振動になったということであり、2倍振動になったということは、振動数が2倍になって波長が半分になったということです（波の速さは変わりません）。
つまり、振動数は
360 × 2 = 720 [Hz]
（問2）
4秒間に8回のうなりが聞こえたということなので、このうなりの振動数は
8 ÷ 4 = 2 [回/s] = 2 [Hz]
求めるおんさの振動数を f1 として、うなり振動数の式（ f = | f1 - f2 |）に各値を代入しますと、
2 = | f1 - 360 |
∴ f1 = 358, 362
弦楽器の音を高くした（振動数を 360Hz より大きくした）ら、うなりはなくなった（弦楽器の振動数がおんさの振動数と同じになった）ということなので、おんさの振動数は 360Hz より大きいということが分かります。つまり、
f1 = 362 [Hz]