磁場を横切る導線

磁場を横切る導線に生じる誘導起電力

『電磁誘導』項では、コイルに発生する誘導起電力について考えましたが、本項では、電気回路の一部の導線（導体棒）が動くときの誘導起電力について考えます。

この話は、『電流が磁場から受ける力』項の話と混同しやすいですが、あちらは磁場の中に電流があると力を受けるという話で、こちらは磁場の中の導線を動かすと電流が発生するという話です。あちらは「電流」→「力」で、こちらは「力」→「電流」です。＊どちらも根本原因はローレンツ力ですが…。
『ローレンツ力＝電流が磁場から受ける力』、『電磁誘導とローレンツ力』項参照。
　閉じる

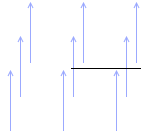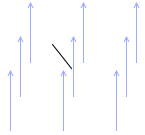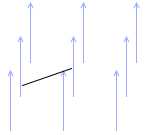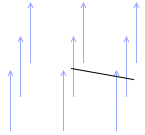
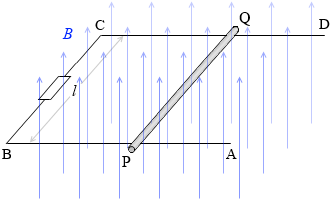磁束密度 B [T] の鉛直上向きの一様な磁場の中に、コの字型の導線ABCDを置き、この上で導体棒PQを動かしたときに発生する誘導起電力について考えます。＊『磁場にすっぽり覆われた中で角度を変えずに動かしても誘導起電力は発生しない』場合との違いはお分かりになりますでしょうか。電流が流れない理由は『磁場の中を動く導体棒は電池』の「ただし、回路全体が磁場の中にある場合」以下で説明しました。四角形のうちの２つの辺において誘導起電力が発生してしまい、打ち消し合って電流が流れないのです。

本項のこの回路では、四角形のうち、PQだけに誘導起電力が発生し、BCでは発生しないので、回路に電流が流れます。
　閉じる

導線ABCDは水平面上にあり、導体棒PQは辺AB、辺CDに接していて、常にそれらに垂直で、速さ v [m/s] の等速で動き、BC間の長さは l [m] であるとします。

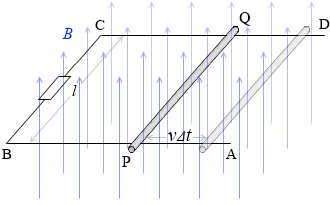導体棒PQが動くと四角形PBCQの面積が変化し、この四角形を貫く磁束の数が変化します。PQは v [m/s] で動いていますので、Δt [s] 間に vΔt [m] だけ進みます。この間、四角形PBCQの面積は ΔS = lvΔt [m²] だけ変化します。

磁束の大きさを Φ [WB] としますと、Φ = BS でありますので、Δt [s] の間に四角形PBCQを貫く磁束は、

　　　　ΔΦ = BΔS = BlvΔt = vBlΔt

だけ、変化します。

ですので、回路PBCQPに発生する誘導起電力 V [V] の大きさは以下のようになります。（ファラデーの電磁誘導の法則の式　V = - N\(\large{\frac{ΔΦ}{Δt}}\)　の N が 1巻きの場合で、向きのことは考えないで大きさのことだけ考えた、つまり - が付かない場合の式　V = \(\large{\frac{ΔΦ}{Δt}}\)　に上の式を代入します。）

　　　　V = \(\large{\frac{ΔΦ}{Δt}}\) = \(\large{\frac{vBlΔt}{Δt}}\) = vBl

誘導起電力の向き

このときの誘導起電力の向きはレンツの法則に従います。

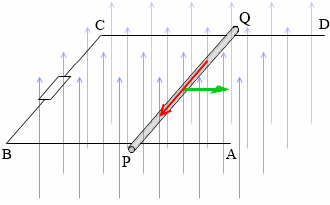左図のような回路において、磁束が鉛直上向きで導体棒PQの移動方向が右向きの場合、上向きの磁束が増えるので、それを打ち消すように、下向きの磁束が増えるような向きに誘導起電力が発生します。その向きは右ねじの法則により、Q→P です。

しかしこのとき、Q→Pの向きに起電力が発生する（電流が流れる）からといって、Q点の方がP点より電位が高いかというとそうではありません。

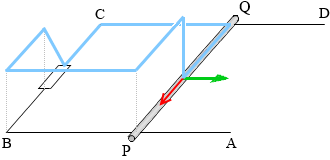電位を水位に例えて図を描くと、左図のようになります。導体棒PQは電池に例えることができ、P点の方が電位が高くなっています。＊電池の内部では電位の低い方から高い方へ電流が流れます。
むしろ別の言い方をすると、電位を引き上げる装置が電池です。
「起電力」という言葉には「電池」「電源」という意味合いが含まれます。
　閉じる

電磁誘導におけるエネルギーの保存

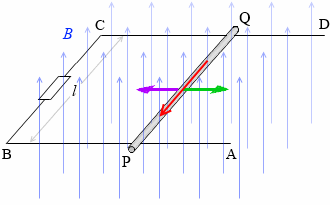手を使って導体棒PQを右に移動させると、QからPへ電流が流れるわけですが、磁場の中の電流は力を受けます。その方向は、フレミングの左手の法則を当てはめて考えてみると、左向きです。

つまり、手で引っ張ろうとすると引き戻されるのです。（レンツの法則です）。ですから、導体棒を等速で動かし続けるには、手に力を入れ続けなければなりません。

発生する電流の大きさを I [A] とすると、引き戻そうとする力の大きさ F [N] は、

　　　　F = IBl

です。これと同じ力で右に引っ張り続けないと導体棒を v [m/s] で動かし続けることはできません。

v で動かし続けたときの、手が導体棒にした仕事 W [J] を求めてみますと、
t 秒間に導体棒は vt [m] 進み、仕事というのは力×距離だから、

　　　　W = F × vt = IBlvt

です。一方、回路PBCQPには電流が流れているのでジュール熱が発生し、その大きさ Q [J] は、

　　　　Q = IVt = IvBlt　　（ 上で示した式 V = vBl より）

です。上の2式を比べると W = Q となっていることが分かります。手がした仕事がそっくりそのまま熱になるのです。エネルギーが保存されているのです。V = vBl という式はエネルギー保存則と矛盾しない式となっています。

斜めに横切る場合

回路が磁場に対して垂直ではなく斜めになっている場合の誘導起電力の大きさを考えてみます。

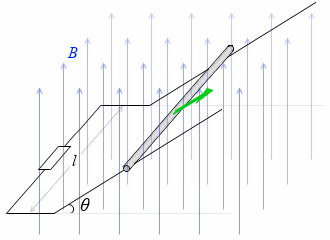水平方向と回路のなす角（仰角）を θ とします。

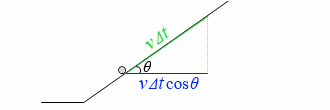そうしますと、磁束を垂直に横切る面積は Δt [s] 間に ΔS = lvΔtcosθ [m²] だけ変化します。磁束を刈り取る面積は ΔS = lvΔtcosθ です。（lvΔtsinθ ではありません）

そして、上で示した水平に横切る場合と同じように計算をしていきますと、

　　　　ΔΦ = BΔS = BlvΔtcosθ = vBlΔtcosθ

　　　　V = \(\large{\frac{ΔΦ}{Δt}}\) = vBlcosθ

となります。水平に横切る場合より小さくなります。

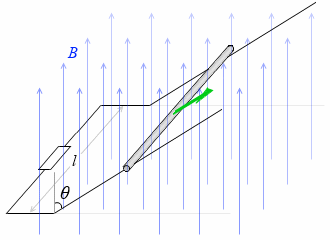もし θ が、左図のような角度として設定されていれば、
V = vBlcosθ でなく V = vBlsinθ となります。sinθ と cosθ の使い分けは間違いやすいです。

磁場を円運動しながら横切る導線に生じる誘導起電力

回路の形が長方形でなく円形で、導体棒が片端を中心にして回っている場合の、導体棒に発生する誘導起電力について考えてみます。

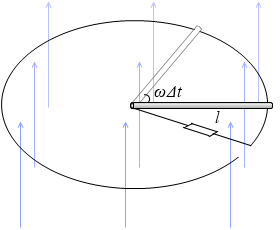鉛直上向きの一様な磁場の中に、半径 l [m] の円形の導線が水平に置かれていて、
片端が円の中心、もう片端が円形導線に接しながら、角速度 ω [rad/s] で等速円運動する導体棒があるとします。

この導体棒は Δt [s] 間に角度 ωΔt [rad] だけ回転します。

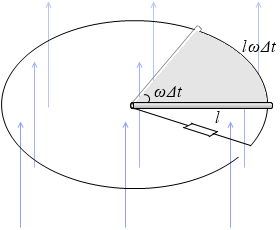この間に導体棒が磁束を掃く（磁束を刈り取る）面積 ΔS [m²] は、左図のような扇型の面積です。

　　　　ΔS = (円の面積) × (割合) = πl² × \(\large{\frac{ωΔt}{2\pi}}\) = \(\large{\frac{1}{2}}\)l²ωΔt

扇型の面積の公式を覚えていらっしゃれば以下のように計算できます。（同じことです…）

　　　　ΔS = \(\large{\frac{1}{2}}\)× (半径) × (弧の長さ) = \(\large{\frac{1}{2}}\)× l × lωΔt = \(\large{\frac{1}{2}}\)l²ωΔt

以下、上で示したように計算をしていきますと、

　　　　ΔΦ = BΔS = B\(\large{\frac{1}{2}}\)l²ωΔt = \(\large{\frac{1}{2}}\)ωBl²Δt

　　　　V = \(\large{\frac{ΔΦ}{Δt}}\) = \(\large{\frac{1}{2}}\)ωBl²

となります。