ミリカンの油滴実験
電子の電気量を求める
J.J. トムソンは電子の電気量と質量の比、比電荷を明らかにしましたが、ミリカン
1868年–1953年のアメリカの物理学者、ロバート・ミリカン。
『プランク定数を求める光電効果の実験』も有名。
は電子の電気量そのものを突き止めました。
その方法は、なるべく小さく軽い帯電物体を電場の中で等速で動かし、その速度から電気量（電荷）を割り出すというものです。
帯電物体としては油滴を用いました 水滴だと蒸発してうまくいかないようです。 。霧吹きで油を噴霧したのです。これにイオン化（電離、帯電）した空気分子を付着させて帯電物体としました。もともと大気にはイオン化した分子がわずかに漂っていますし噴霧したときの摩擦でも油滴は帯電するものですが、ミリカンは放射線（X線等）を当てて空気分子をイオン化しました。
その油滴を電場の中で等速度運動（等速直線運動）をさせます。等速度運動するということは油滴にはたらく力がつり合っている（合力が 0 ）ということであり、つり合いの式を立てることができます。
加速度を測定して運動方程式を立ててもいいのですが、加速度を正確に測定するのは大変です。
（まあ、つり合いの式は運動方程式であるとも言えるのですが）
ミリカンの油滴実験
ミリカンは以下のような装置を作って油滴の実験をしました。
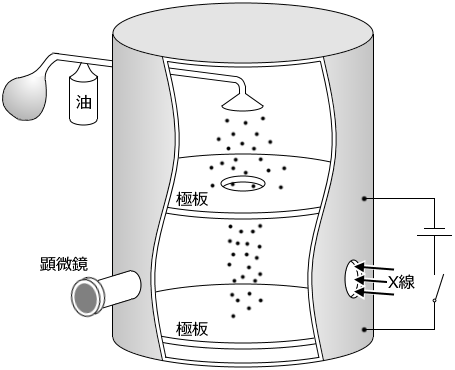霧吹きで小さな油滴を作り、極板中央の小さな穴から落下させます。そしてX線を当ててイオン化した空気分子を油滴に付着させ、帯電させます。
落下していく油滴は空気抵抗を受け速度が一定になります。油滴は重力によって加速しますが、軽いので空気抵抗を受けすぐに終端速度に達します。
すぐに終端速度に達するということは
終端速度が小さいということです。
ゆっくり下降するということです。
極板間に電圧を掛ければ油滴は（重力、空気抵抗以外に）さらに静電気力（クーロン力）を受けるので終端速度は変わります。
イオンの電気量によって終端速度は
大きくなるかもしれませんし
小さくなるかもしれませんし
0 になるかもしれませんし
逆向きになるかもしれません。
逆向きになるというのは、
電圧を掛ける向きを逆にする場合もありますし、
油滴の電荷についても正の場合と負の場合、両方あるからです。
個々の油滴について、電圧を掛けた場合と掛けない場合の終端速度を顕微鏡を覗いて測定します。
トムソンが電場と磁場を使って比電荷を求めたのに対して、
ミリカンは電場と重力場を使って電気素量を求めた、といえます。
油滴の質量を \(m\) [kg] 、重力加速度の大きさを \(g\) [m/s2] 、空気抵抗の比例定数を \(k\) 、電圧を掛けないときの終端速度の大きさを \(v_0\) [m/s] 、電圧を掛けたときの終端速度の大きさを \(v_1\) [m/s] 、油滴の電気量の大きさを \(q\) [C] 、極板間の電場の強さを \(E\) [V/m]
掛けた電圧が \(V\) [V] で、極板間の距離が \(d\) [m] であれば
\(E\) = \({\large\frac{V}{d}}\) です。
あと、[V/m] = [N/C] です。
、電場の方向は鉛直方向、とします。
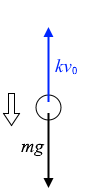（電圧を掛けない場合）
つり合いの式は
\(mg\) = \(kv_0\) ……①
となります。
厳密には、この他に浮力も考慮しなければなりませんが、
浮力は空気抵抗に比べてとても小さいのでここでは無視します。
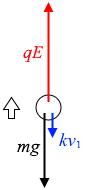（電圧を掛けて上昇した場合）
\(E\) の電場の中の \(q\) の電荷が受ける力は \(qE\) であり、空気抵抗は運動方向とは逆向きにはたらくから、つり合いの式は
\(qE\) = \(mg + kv_1\) ……②
となります。
電圧を掛けたときに下降するパターンもあります。
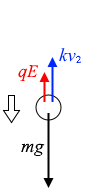\(mg\) = \(qE\) + \(kv_2\)
こんな感じのときや
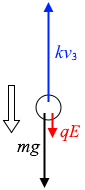\(mg + qE\) = \(kv_3\)
こんな感じのときです。
もっといえば、電圧を調整して油滴を静止させることもできます。
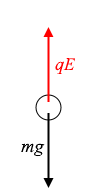
速度が 0 であるので \(kv\) = 0 であり、
\(mg\) = \(qE\)
となります。
油滴の質量 \(m\) については、その半径から割り出します。油滴はきれいな球形をしており、半径を \(r\) [m] とすると体積は \({\large\frac{4}{3}}\pi r^3\) [m3] であり
測定するのはイオン化した空気分子が付着した油滴であるわけですが、空気分子は油滴に比べて非常に小さいので無視します。
または、空気分子が付着しなくとも油滴に電子が付いたり電子を失ったりして帯電することもありえます。
、それに油の密度 \(ρ\) [kg/m3] を掛けると質量になります。
\(m\) = \({\large\frac{4}{3}}\pi r^3ρ\) ……③
そうしますと、①式 \(mg\) = \(kv_0\) において \(m\) と \(g\) が定まったことにより \(v_0\) を測定すれば \(k\) が求められることになります。
\(ρ\) については、油を大きい容器に入れて質量と体積を測ればいいので割り出すのは簡単ですが、
油滴の半径 \(r\) は小さいので測定は困難です。
実際には
\(kv\) = \(6πηrv\)
というストークスの法則の式から \(r\) を割り出します。
\(k\) というのは \(6πηr\) のことなのです。
\(η\)（イータ）は空気の粘性率です。
この \(k\) = \(6πηr\) と③式を①式 \(mg\) = \(kv_0\) に代入すると
\({\large\frac{4}{3}}\pi r^3ρg\) = \(6πηrv_0\)
∴ \({\large\frac{4}{3}}\pi r^2ρg\) = \(6πηv_0\)
∴ \({\large\frac{4}{3}}r^2ρg\) = \(6ηv_0\)
∴ \(r^2\) = \({\large\frac{9}{2}}{\large\frac{ηv_0}{ρg}}\)
もし浮力も考慮するとなると、浮力は
\(f_\rm{浮}\) = \({\large\frac{4}{3}}\pi r^3ρ_0g\) （\(ρ_0\) は空気の密度）
であり、①式は
\(mg\) = \(kv_0 + f_\rm{浮}\)
となり、上と同じように解いていくと、
\({\large\frac{4}{3}}\pi r^3ρg\) = \(6πηrv_0 + {\large\frac{4}{3}}\pi r^3ρ_0g\)
∴ \({\large\frac{4}{3}}\pi r^2(ρ-ρ_0)g\) = \(6πηv_0\)
∴ \({\large\frac{4}{3}}r^2(ρ-ρ_0)g\) = \(6ηv_0\)
∴ \(r^2\) = \({\large\frac{9}{2}}{\large\frac{ηv_0}{(ρ-ρ_0)g}}\)
となります。
つまり油滴の半径は終端速度から求められるということです。
ですが、ストークスの法則は高校物理ではなく大学物理の範囲です。
ミリカンの油滴実験は高校の理科実験として行うにはちょっと難易度が高いです。
そして、②式 \(qE\) = \(mg + kv_1\) により \(v_1\) を測定すれば \(q\) が特定できることになります。
このことは、①式を②式に代入して、
\(qE\) = \(mg + kv_1\)
= \(kv_0 + kv_1\)
= \(k\)(\(v_0 + v_1\))
∴ \(q\) = \({\large\frac{k}{E}}\)(\(v_0 + v_1\))
という式の右辺に各値を代入して \(q\) を求めるということでもあります。